2. ¿Éxito o fracaso?
Cuando partimos una sandía o abrimos cualquier otra fruta, podemos encontrarnos con que esté buena (éxito) o, por el contrario que esté podrida (fracaso).
Este ejemplo, esconde detrás un tipo de variable aleatoria que se repite con mucha frecuencia en nuestra vida diaria y que el matemático suizo Jakob Bernoulli ya observó e investigó a principios del siglo XVIII. Es por ello que estos experimentos aleatorios lleven el nombre de distribuciones de Bernouilli.
|
|
Sandía. Foto de Daquella manera con licencia by-2.0-deed
|
Un experimento aleatorio es de tipo Bernouilli cuando sólo se pueden dar dos resultados posibles (normalmente los llamaremos éxito y fracaso). Algunos ejemplos son:
- Responder a una pregunta con dos opciones (Sí/No) al azar y acertar (éxito) o fallar (fracaso).
- Una familia quiere que su futuro bebé sea chica. Chica (éxito) y chico (fracaso)
- ¿Tiene el cabello rubio? Sí (éxito) , No (fracaso)
- Lanzar un dado y que salga un valor mayor que 4. Si sale un 5 o un 6 (éxito), si sale cualquier otro valor (fracaso)
Hay que entender que éxito y fracaso son palabras (etiquetas) que usamos para los resultados y no debemos interpretarlas literalmente ya que pueden significar cosas distintas, en función del contexto del problema con el que estemos trabajando.
Por ejemplo, si estamos comprobando si un tornillo es defectuoso; si lo es será un éxito y si no lo es será un fracaso. Pero puede ocurrir el caso contrario, estamos comprobando si un tornillo está perfectamente fabricado y no presenta defectos, por lo que si está correcto será un éxito y si presenta defectos, imperfecciones, será un fracaso.
Actividad
Una distribución de Bernouilli es una variable aleatoria discreta que sólo puede tomar dos valores, 0 y 1. Normalmente, el fracaso se asocia con el valor 0 y el éxito con el 1.
Se nombra como Be(p), donde p(X=1) = p es la probabilidad de obtener éxito y p(X=0) = q = 1-p la probabilidad obtener fracaso.
Sus parámetros son:
- Media o esperanza matemática:
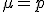
- Varianza:
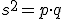
- Desviación típica:
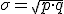
Normalmente, no realizamos una experimento una única vez sino que, por decirlo de algún modo, lo hacemos de manera repetida (por lotes). Cuando realizamos un lote, es decir, cuando repetimos una serie de experimentos Bernouilli idénticos, aparecerá la distribución binomial que veremos más adelante.
A continuación, vamos a experimentar con algunas actividades relacionadas con distribuciones Bernouilli.
Ejemplo o ejercicio resuelto
|
|
|
Un recipiente contiene 2 bolas amarillas y 6 bolas rojas. Introducimos la mano en él y sacamos una bola. Vemos si es amarilla y la introducimos de nuevo en la urna.
¿Es un experimento de tipo Bernouilli? En caso afirmativo, ¿cuál sería el éxito y cual el fracaso?
¿Cúal es la probabilidad de sacar una bola amarilla? ¿y de sacar una roja?
AV - Pregunta de Elección Múltiple
Selecciona la opción correcta en cada uno de los casos:
(1) Estamos realizando un control de calidad y tenemos un lote de tornillos fabricados por una máquina que, por término medio, produce un 3% de defectuosos. Extraemos uno de ellos al azar, ¿cuál es la probabilidad de que éste sea defectuoso?
|
(a) Depende de si ha sido fabricado durante la noche.
| |
|
(b) 0,03
| |
|
(c) 0,97
|
|
(a) 0,95
| |
|
(b) 0,05
| |
|
(c) 1,2
|
AV - Actividad de Espacios en Blanco
Completa las huecos que faltan en el siguiente texto, sobre las distribuciones Bernouilli, usando las palabras que figuran en la siguiente lista.
| varianza | infinitos |
fracaso | desviación |
binomiales | discreta |
0 |
p |
Una distribución de tipo Bernouilli es una variable aleatoria . Por tanto, éste tipo de variables no pueden tomar valores.
Concretamente, sólo toman dos valores: 1 y que llamaremos, normalmente, éxito y , respectivamente.
La repetición de experimentos Bernouilli idénticos darán lugar a las distribuciones .
Como las variables de tipo Bernouilli son discretas podemos calcularle sus parámetros: media o esperanza matemática, varianza y típica. Si tenemos una variable Be(p), su media vale y su vale p·q