1.3. Parámetros en vez de medidas
En la Unidad en la que se desarrolla el estudio de las variables estadísticas, se explica cómo calcular las medidas asociadas a una de estas variables: media, mediana, varianza o desviación típica.
A las variables aleatorias (que estamos estudiando en esta unidad) también le calcularemos medidas.
Incluso, coincidirán con los nombres de las medidas de las variables estadísticas. Es por ello que, para evitar confusiones, en vez de medidas, utilizaremos el nombre de parámetros.
|
|
|
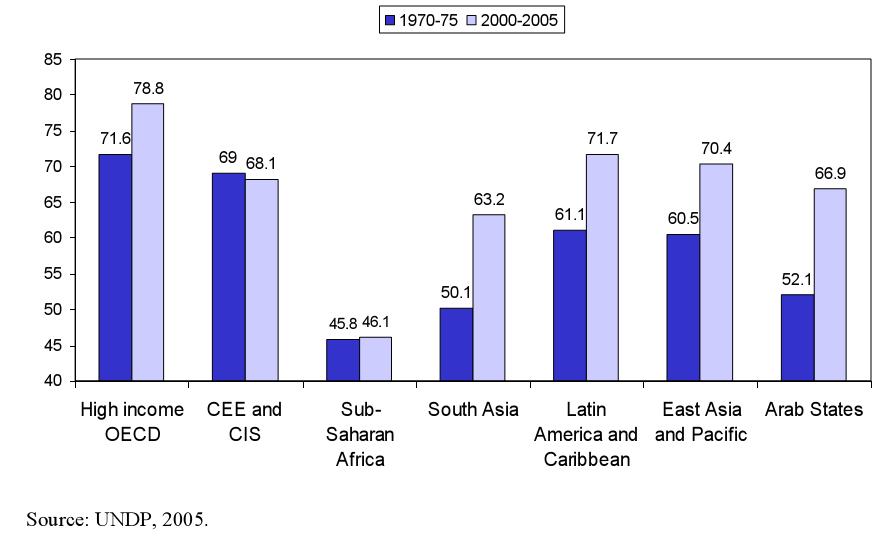
"Esperanza de vida al nacer" gráfico incluido en un informe de la Comisión sobre los Determinantes Sociales de la Salud encargado por la OMS |
Ya hemos visto que las funciones asociadas a una variable aleatoria nos informan sobre ella.
También hemos indicado en el párrafo anterior, que a las variables aleatorias se les pueden calcular una serie de medidas que llamaremos parámetros. Pero, ¿qué utilidad tienen estos parámetros?
Pues diferenciar unas variables aleatorias de otras porque, las variables aleatorias, al igual que las personas no son todas iguales.
Dos personas distintas tienen también distinto DNI, color de ojos, de pelo, peso, altura ... Y también nuestra esperanza de vida (los años que esperamos vivir) depende de muchos factores. Puede variar, entre otros condicionantes, de si vivimos en un país desarrollado o en uno subdesarrollado.
Del mismo modo, dos variables aleatorias distintas tendrán como norma general valores distintos en sus parámetros.
Dada una variable aleatoria discreta, X, que toma los valores: x1, x2, x3, ... , xk y dada su función de probabilidad asociada:
p(X=xi) = pi, podemos calcularle los siguientes parámetros, cuyas fórmulas se detallan:
-
Media o esperanza matemática:
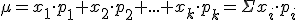 (También se representa como E(x))
(También se representa como E(x))
Puede interpretarse como el valor esperado o medio que toma la variable o, tambien, como el valor central de la distribución.
- Varianza:
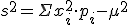 (También se representa con Var(X) o V(x))
(También se representa con Var(X) o V(x))
- Desviación típica:
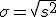 (También se representa por DT(x))
(También se representa por DT(x))
Vamos a poner en práctica el cálculo de parámetros de la variable aleatoria discreta que controla el movimiento de los caballos participantes en la carrera de nuestro juego.
Recordamos el juego: "Tenemos 12 caballos (numerados del 1 al 12), lanzamos dos dados y sumamos las cantidades obtenidas en cada uno de ellos. Finalmente, avanza una posición el caballo cuyo número coincida con el valor de dicha suma".
Hemos visto que cada uno de los parámetros se calcula mediante una fórmula. Para facilitar el trabajo de aplicación de las fórmulas es conveniente elaborar una tabla como la que se indica, donde además de las dos filas que contienen los valores de xi y de pi, figuren dos filas más con los valores de xi·pi y de xi2·pi y tambien una columna con las sumas de los valores de cada una de las filas.
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
8 |
9 |
10 |
11 |
12 | Sumas |
| pi | 0/36 |
1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 |
5/36 | 4/36 |
3/36 |
2/36 |
1/36 |
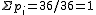 |
| xi·pi | 0/36 |
2/36 | 6/36 | 12/36 |
20/36 | 30/36 |
42/36 |
40/36 |
36/36 | 30/36 | 22/36 | 12/36 |
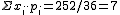 |
| xi2·pi | 0/36 | 4/36 | 18/36 |
48/36 | 100/36 | 180/36 | 294/36 |
320/36 |
324/36 |
300/36 | 242/36 |
144/36 |
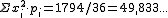 |
 |
|
Foto de jlastras con licencia by-2.0-dee |
Una vez elaborada la tabla, obtener los valores de los parámetros es pan comido. Basta aplicar las fórmulas:
- Esperanza:
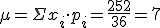
- Varianza:
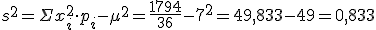
- Desviación típica:
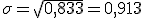
Una compañía aérea ha vendido 153 billetes para un avión de 148 pasajeros, considerando que, finalmente algunos no acudirán al aeropuerto a realizar su viaje.
Si llamamos X: "Número de pasajeros que acuden finalmente al aeropuerto para viajar en el avión", la distribución de esta variable se recoge en la siguiente tabla:
|
xi |
146 |
147 |
148 |
149 |
150 |
151 |
152 |
153 |
|
pi |
0,06 |
0,08 |
0,14 |
0,21 |
0,23 |
0,18 |
0,08 |
0,02 |
Observa que pi es la probabilidad de que finalmente acudan xi pasajeros para viajar en el avión. Por ejemplo, a la vista de los datos de la tabla, la probabilidad de que acudan finalmente 150 pasajeros es 0,18 (un 18%).
Responde a las siguientes cuestiones:
Cuestión 1: X es una variable aleatoria ...
|
(a) Discreta
| |
|
(b) Continua
|
Cuestión 2: La probabilidad de que todos los viajeros que acuden al aeropuerto tengan plaza en el avión vale ...
|
(a) 0,14
| |
|
(b) 0,32
| |
|
(c) 0,28
|
Cuestión 3: La probabilidad de que se quede sin plaza alguno de los viajeros que van al aeropuerto vale ...
|
(a) 1
| |
|
(b) 0,72
| |
|
(c) 0,15
|
Cuestión 4: El número esperado de viajeros que acudirán al aeropuerto es ...
|
(a) 151,2
| |
|
(b) 154
| |
|
(c) 149,43
|
¡Nuestra intuición nos juega malas pasadas. Cuidado con ella!
Un ejemplo de ello lo proporciona el Problema (o Paradoja) de Monty Hall, que muestra muy a las claras cómo fallamos a la hora de calcular probabilidades.
| Probabilidad poco intuitiva. Serie Numb3rs |
El Problema de Monty Hall está inspirado en un concurso televisivo estadounidense y lleva el nombre del presentador de dicho concurso. Let's Make a Deal (Hagamos un trato), es el nombre del programa y fue emitido entre los años 1963 y 1986.
Consiste en lo siguiente:
El concursante escoge una puerta de entre tres posibles y consigue el premio que se encuentra detrás de la puerta elegida.
Una de estas puertas tiene un coche y las otras dos una cabra. Una vez que el concursante ha elegido su puerta, el presentador que conoce la puerta que tiene el premio, antes de abrirla y ver lo que le ha tocado al concursante, abre una de las otras dos puertas mostrando que detrás de ella hay una cabra.
Hecho ésto, ofrece al concursante la posibilidad de cambiar la puerta que elegió al principio, por la otra que queda sin abrir, generando indecisión en el concursante y dando emoción al juego.
¿Qué crees que debería hacer el concursante? ¿Mantener la opción elegida al principio o coger la puerta que queda sin abrir? ¿Que opción consideras que tiene más probabilidades de ganar?
Opción 1: Quedarse con la puerta elegida al principio.
Opción 2: Cambiar a la puerta que queda sin abrir.
Opción 3: Da igual, cambiar o no cambiar.
En principio, nuestra intuición nos lleva a pensar que es evidente y muy claro que da igual (Opción 3). La intuición nos dice que quitando una puerta sin premio, la puerta elegida al principio tiene un 50% de probabilidad de tener el coche y el 50% de tener una cabra. Por tanto, da igual cambiar que no cambiar. Pero, resultaría demasiado simple y sencillo para ser una paradoja o problema si fuera tan fácil, ¿verdad?
En este vídeo de la serie Numb3rs lo explican bastante bien, pero tambien puedes experimentar con el simulador que se te ofrece en el siguiente enlace:
Simulador del Problema de Monty Hall

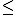 148
148
 = (1278,96 + 1728,72 + 3066,56 + 4662,21 + 5175 + 4104,18 + 1848,32 + 468,18) - 149,432
= (1278,96 + 1728,72 + 3066,56 + 4662,21 + 5175 + 4104,18 + 1848,32 + 468,18) - 149,432