2.2. Entre binomios anda el juego
En multitud de ocasiones no realizamos una experimento una sola vez sino que, por decirlo de algún modo, lo hacemos de manera repetida (por lotes).
Cuando realizamos un lote, es decir, cuando repetimos una serie de experimentos Bernouilli idénticos, aparece la distribución binomial.
Binomial
Para saber si una variable aleatoria sigue una distribución binomial debemos ver si se cumplen las siguientes condiciones:
(1) Hay un experimento aleatorio que se repite n veces de modo independiente. (Ejemplo: Lanzar una moneda n=10 veces y obtener cara o cruz, en cada lanzamiento, es independiente del resultado que hayamos obtenido en el lanzamiento anterior)
(2) Cada vez que realizamos el experimento sólo pueden darse dos situaciones, variable aleatoria Bernouilli: éxito o fracaso (Ejemplo: obtener cara o cruz. Llamar: éxito o fracaso dependerá de lo queramos obtener. Si queremos contar el número de caras que han salido en los n lanzamientos, cada vez que salga cara lo consideraremos como un éxito).
(3) La suma de las probabilidades del éxito y del fracaso deben sumar uno, pero no tienen que valer lo mismo. (Ejemplo: en el caso de cara o cruz ambas probabilidades valen 1/2, aunque en general no tienen por qué ser iguales)
p = probabilidad de obtener éxito
q= 1-p = probabilidad de no obtener éxito, esto es, de obtener fracaso.
Entonces, diremos que la variable que se define como el número de éxitos conseguidos:
X = "número de éxitos conseguidos al realizar los n experimentos",
es una distribución binomial y la llamaremos B(n,p), donde n es el número de veces que realizamos el experimento y p es la probabilidad de obtener éxito.
Como vimos en el apartado 1.2., dada una variable aleatoria existen varias funciones asociadas a ella. Una de estas funciones es la función de probabilidad.
Vamos a intentar deducir, mediante un ejemplo, la función de probabilidad de una distribución binomial.
 |
| Imagen de Marianne Perdomo con licencia by-sa-2.0-dee |
Se ha obtenido mediante un control de calidad efectuado en una empresa dedicada a la fabricación de candados y cerraduras que, el 20% (0,2) de las cerraduras producidas por una determinada máquina son defectuosas (tienen algún tipo de imperfección y no funcionan correctamente). Entre las 10:00 y las 10:15 de la mañana de ayer, dicha máquina produjo 3 cerraduras.
Vamos a analizar la variable aleatoria X= "número de cerraduras en perfecto estado" con las 3 cerraduras fabricadas.
Llamaremos C (cerradura en perfecto estado) y D (cerradura defectuosa).
Con los datos que tenemos, la probabilidad de que al elegir una cerradura al azar fabricada por esta máquina esté en perfecto estado (C) o sea defectuosa (D) son 0,8 y 0,2 respectivamente:
p(C)=0,8 y p(D)=0,2
Como sólo hay dos resultados posibles para la cerradura, en perfecto estado (C) o defectuosa (D), experimento Bernouilli, y realizamos el experimento (fabricar una cerradura) un lote de veces, tenemos que la variable X se trata de una B(3; 0,8).
Vamos a recoger en una tabla todos los resultados posibles que nos podemos encontrar al probar las 3 cerraduras y calcularemos las probabilidades de X.
|
Resultados
(1ª,2ª,3ª) |
Probabilidad p(C)=0,2 y p(D)=0,8 |
Nº de éxitos (X)
Contamos: "Nº de cerraduras en perfecto estado (C)"
|
| DDD | (0,2)·(0,2)·(0,2)=0,008 | X=0 |
| DDC | (0,2)·(0,2)·(0,8)=0,032 | X=1 |
| DCD | (0,2)·(0,8)·(0,2)=0,032 | X=1 |
| CDD |
(0,8)·(0,2)·(0,2)=0,032 | X=1 |
| DCC | (0,2)·(0,8)·(0,8)=0,128 | X=2 |
| CDC | (0,8)·(0,2)·(0,8)=0,128 | X=2 |
| CCD | (0,8)·(0,8)·(0,2)=0,128 | X=2 |
| CCC | (0,8)·(0,8)·(0,8)=0,512 | X=3 |
Agrupando los resultados según los valores que toma la variable X, su función de probabilidad sería la siguiente:
| xi | 0 |
1 |
2 |
3 |
| pi=p(X=xi) | 0,008 | 3·0,032 =0,096 | 3·0,128 = 0,384 |
0,512 |
Si fijamos nuestra atención y observamos con detalle la tabla de de resultados veremos que es posible calcular las probabilidades como sigue:
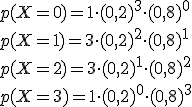
Vamos a analizar la siguiente probabilidad, justificando qué significa cada número:
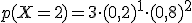
3 indica el número de casos en que puede ocurrir que haya 2 cerraduras correctas (X=2). Basta ver la tabla y contar cuántas veces ocurre.
0,8 es la probabilidad de que una cerradura esté en perfecto estado (éxito) y está elevado a 2.
0,2=1-0,8 es la probabilidad que una cerradura esté defectuosa (fracaso) y está elevado a 1. (Total - Nº de éxitos = Nº de fracasos)
Pero, ¿y si tenemos un número n de cerraduras en vez de sólo 3? ¿Cómo calculamos la probabilidad de obtener k cerraduras en perfecto estado?
Bastará usar la fórmula:
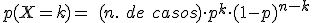
Y para calcular el número de casos en que se pueden obtener k éxitos al realizar n experimentos deberemos hacer uso del número combinatorio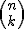 
que ya tratamos en el apartado anterior.
Por tanto, con todo ésto podemos afirmar que:
Función de probabilidad
La función de probabilidad de una variable aleatoria binomial B(n,p) viene dada por:
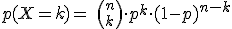
| Proyecto Descartes. Ministerio de Educación. |
AV - Pregunta Verdadero-FalsoEn todos los apartados de ejercicio consideraremos que tenemos una distribución binomial, B(5;0,2)
Con la ayuda de la escena anterior, o bien realizando los cálculos de manera manual, calcula las probabilidades indicadas y selecciona Verdadero o Falso según corresponda.
Verdadero Falso
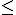3)=0,72
