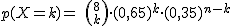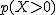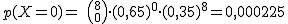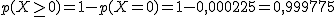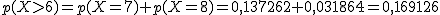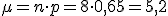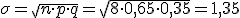2.3. Los rasgos característicos de la Binomial
De la misma manera que a cada uno de nosotros nos definen o cararacterizan unas facciones o rasgos determinados, las variables aleatorias también presentan una serie de propiedades características que las distinguen de las demás. Estas señas de identidad, como ya comentamos en el apartado 1.3 de esta Unidad, se denominan parámetros de la variable aleatoria.
Si X es una variable aleatoria binomial B(n,p), sus parámetros asociados se pueden calcular facilmente con las siguientes fórmulas:
-
Media o esperanza matemática:
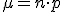 (También se representa como E(x))
(También se representa como E(x))
Puede interpretarse como el valor esperado o medio que toma la variable o, tambien, como el valor central de la distribución.
- Varianza:
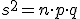 (También se representa con Var(X) o V(x))
(También se representa con Var(X) o V(x))
- Desviación típica:
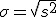 (También se representa por DT(x))
(También se representa por DT(x))
En el apartado anterior estuvimos trabajando con la variable aleatoria X= "número de cerraduras en perfecto estado" producidas por una determinada máquina de una fábrica de candados y cerraduras.
La tabla que nos daba la función de probabilidad de la variable X era la que se muestra a continuación:
| xi | 0 |
1 |
2 |
3 |
| pi=p(X=xi) | 0,512 | 0,384 | 0,096 | 0,008 |
Además, vimos que la variable X seguía un modelo de distribución binomial B(3;0,8)
Vamos a calcular los parámetros de esta variable. Para ello basta observar que: n=3 p=0,8 q=0,2 y aplicar las fórmulas correspondientes:
| Media o esperanza matemática: |
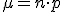 |
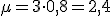 |
| Varianza: | 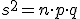 |
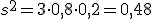 |
| Desviación típica: | 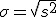 |
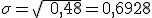 |
¿A que no es tan difícil? Pues con los parámetros concluimos todos los contenidos relativos al trabajo con binomiales.
La dificultad en el trabajo con distribuciones binomiales, casi siempre, está en los problemas donde, tras leer el enunciado, debes reconocer si es una distribución binomial o no lo es y, en este caso, identificar los valores de n y de p.
A continuación se muestra un resumen que contiene los atributos más importantes de este tipo de distribuciones.
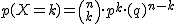
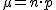
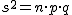
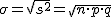
|
|
Aritmética por My Buffo con licencia by-2.0-deed |
En una determinada universidad española, sólo el 65% de los estudiantes que inician los estudios en el grado en Matemáticas concluyen finalmente esta titulación. El resto, cambian de estudios dedicándose a otros, o bien abandonan definitivamente sus carreras universitarias.
De un grupo de ocho estudiantes elegidos al azar, halla la probabilidad de que concluyan sus estudios en Matemáticas:
(a) Alguno de ellos.
(b) Más de seis.
(c) Calcula la media (número esperado) de estudiantes que terminarán la carrera.
(d) Calcula la desviación típica.
En el siguiente enlace accederás a la página de Vitutor donde podrás repasar, consolidar y ampliar los contenidos de la distribución binomial.
La página contiene resumen de los conceptos y fórmulas más importante y ejercicios y problemas resueltos.
Desde esa misma página podrás acceder a esta otra, también de Vitutor, donde podrás repasar aún más, si fuese necesario.