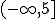2.2. Soluciones: Interpretación
Hemos indicado anteriormente que las soluciones de una inecuación son puntos de una semirrecta de la recta real.
-
Si el símbolo de desigualdad de la ecuación es estricto, es decir, es un
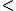 o un
o un 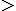 . entonces el extremo numérico de la semirrecta no es una solución de la inecuación. (Ver primer apartado de la autoevaluación anterior)
. entonces el extremo numérico de la semirrecta no es una solución de la inecuación. (Ver primer apartado de la autoevaluación anterior)
-
Si el símbolo de desigualdad de la ecuación no es estricto, es decir, es un
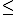 o un
o un 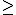 . entonces el extremo numérico de la semirrecta si es una solución de la ecuación. (Ver segundo apartado de la autoevaluación anterior)
. entonces el extremo numérico de la semirrecta si es una solución de la ecuación. (Ver segundo apartado de la autoevaluación anterior)
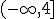 es la solución de
es la solución de 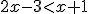
Verdadero Falso
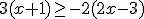 es el intervalo
es el intervalo 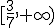
Verdadero Falso
(a) 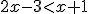
(b) 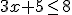
(c) 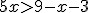
(d) 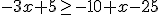
Ayuda: debes realizar las transformaciones previas en cada una de la inecuaciones hasta obtener ax + b < c, o una cualquiera de las otras tres desigualdades.
Una vez tengas ésto, cambia en el applet los
valores de a, b, c y el signo de relación (signo de desigualdad) y compara los resultados
que
has obtenido con los que te ofrece el applet.
Jesús es el chico de mayor edad de un equipo de fútbol de categoría infantil. Es un poco bromista y además está bien preparado en Matemáticas.
Ante la pregunta realizada por el nuevo entrenador: "¿cuántos años tienes?" le responde: “El doble de mi edad más dos años es mayor que mi edad más 14 años”.
Con esta pista el nuevo entrenador no puede obtener la edad de Jesús, pero ¿puede averiguar que edad como mínimo tiene Jesús?
De la misma manera que hemos acometido la resolución de inecuaciones con la ayuda de applet de Geogebra, también podemos hacerlo con la ayuda de otro programa de cálculo simbólico y numérico, bastante potente. Se trata de Wiris.
Al igual que ocurre con Geogebra, Wiris no resuelve los problemas que se nos puedan plantear. Nosotros tenemos que entender el enunciado, adivinar qué se nos pide, decidir quién es la incógnita, plantear la ecuación, inecuación. En ese momento es cuando entran en escena estas herramientas, ellas son las que resuelven la ecuación o inecuación. Aún nos queda comprobar si la solución obtenida tiene sentido en el contexto del problema planteado, y se ajusta a las condiciones impuestas.
A continuación, tienes una presentación, dónde se explican cómo resolver inecuaciones con Wiris.
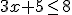 Solución:
Solución: 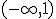
Verdadero Falso
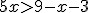 Solución:
Solución: 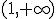
Verdadero Falso
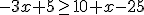 Solución:
Solución: 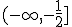
Verdadero Falso
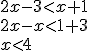
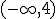
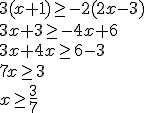
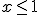 , que expresado en forma de intervalo sería:
, que expresado en forma de intervalo sería: 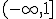
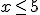 , que expresado en forma de intervalo sería:
, que expresado en forma de intervalo sería: