2.1. Inecuaciones
Foto de sugree con licencia by-sa 2.0 de
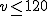Si eres un buen conductor seguro que sabes que en las autopistas españolas debemos circular a una velocidad inferior o igual a 120 km/h.
Si llamamos v, a la velocidad en kilómetros por hora a la que conducimos, la expresión algebraica que representa esa situación vendría dada por: .

Si circulamos a velocidad superior a 120 km/h estaremos poniendo en peligro nuestra seguridad y seremos sancionados. En este caso la expresión algebraica sería: .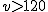

Las dos expresiones anteriores se denominan inecuaciones o desigualdades.
Lo primero que llama la atención de las inecuaciones es que tienen infinitas soluciones. Esa es una característica esencial de las inecuaciones.
 
Trabajaremos exclusivamente con inecuaciones de una incógnita.
Icono IDevice Actividad

Una inecuación es una expresión matemática con cifras y letras caracterizada por tener alguno de los signos de desigualdad (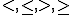), mostrando un desequilibrio entre cifras y letras.

Una inecuación respeta todas las propiedades vistas para las desigualdades numéricas, que son:

- No cambia de sentido, si se suman o restan números a ambos miembros, ya sean positivos o negativos.

- Tampoco cambia de sentido, si se multiplican o dividen ambos miembros por un número positivo.

- Cambia de sentido, se desequilibra hacia el otro lado, si se multiplican o dividen ambos miembros por un número negativo.


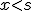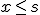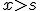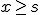Icono IDevice Actividad
Resolver una inecuación es encontrar el conjunto de números reales que cumplen la desigualdad. Este conjunto infinito de soluciones será un intervalo de la recta real.

El proceso de resolución consiste en realizar tranformaciones (suma, resta, multiplicación o división) de una misma cantidad a ambos miembros de una inecuación, hasta llegar a una inecuación en la que la incógnita esté sóla en uno de sus miembros, en el otro haya un número y, entre ambos, uno de los signos de desigualdad.

El objetivo de estas transformaciones es llegar a obtener uno de los siguientes modelos (donde x es la incógnita y s un número real)




Finalmente, la solución de la inecuación vendrá dada por los infinitos valores que verifican esta última desigualdad. Es decir, todos los puntos del intervalo que tienen por extremo inicial (o final) al valor s.

Icono de iDevice AV - Reflexión
En la siguiente escena de Descartes, debes asociar a cada inecuación que aparece en la primera columna la desigualdad que le corresponda de la última columna.
Esta unidad interactiva requiere la máquina virtual de Java J2RE.

« Anterior | Siguiente »