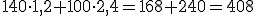4.2. Lo más importante: planificar
 |
| 2. Imagen de Petezin con licencia Creative Commons. |
Siguiendo con el símil culinario que hemos utilizado en algunos apartados, cuando vas a preparar un plato, a veces tienes que elegir qué condimentos e ingredientes vas a utilizar. Por ejemplo, si vas a hacer un puchero, no es lo mismo utilizar carne de ternera que de cerdo, añadir un hueso blanco o un buen hueso de jamón, y seguro que se te están ocurriendo más opciones.
En la resolución de problemas pasa lo mismo. Lo más importante es elegir bien las incógnitas que vamos a utilizar, ya que dependiendo de elección puede ser más simple o complicado plantear y resolver las ecuaciones necesarias.
 |
Por ejemplo, Juan tiene un primo mayor que él que tiene tres hijas. Como no quería alargar mucho la época de tener niños pequeños, las tres hijas nacieron en años consecutivos. Si la suma de las tres edades de las niñas es la actualidad es 36, ¿cómo podríamos saber que edad tiene cada una?
Está claro que las edades de las tres hijas son números consecutivos, podemos considerar que x es la edad de la menor, x+1 la de la mediana y x+2 la de la mayor. Si sumamos sus tres edades nos da 3x+3.
Pero hay otro camino para plantear el problema, y es considerar que la edad de la mediana es x, la de la menor x-1 y la de la mayor x+1. En este segundo caso, al sumar las tres edades nos da 3x, por lo tanto, la edad de la mediana es la tercera parte del total, es decir, 12 años y sus hermanas tienen 11 y 13 años respectivamente.
La mañana en la tienda de ropa ha estado animada. Juan ha vendido un total de 20 prendas entre pantalones marcados a 50 € y camisas cuyo precio está fijado en 30 €. Al cerrar al mediodía, ha comprobado que ha recaudado un total de 760 €. Queremos saber cuántos pantalones y camisas ha vendido.
Método de resolución 1
Si llamamos "x" al número de pantalones vendidos e "y" al de las camisas, plantea el sistema de ecuaciones correspondiente y encuentra la solución por el método que te resulte más cómodo.
Método de resolución 2
Vamos ahora a resolver el problema con una sóla incógnita. Si llamamos x al número de pantalones, sabemos que el número de camisas vendidas es 20-x. Plantea ahora la ecuación que relaciona esas dos expresiones y resuélvela para encontrar cada valor.
A Juan le han llegado los recibos del Impuesto de Bienes Inmuebles (IBI), tanto del local comercial como de su vivienda. El importe en euros que debe pagar es el resultado de multiplicar la superficie en metros cuadrados del inmueble por un coeficiente que depende de varios factores: tipo de inmueble, zona de la ciudad en que se ubica, etc. El local mide 100 m2, en tanto que su vivienda tiene 140 m2. Por sus dos propiedades debe pagar en total 408 euros.
Juan desea saber qué coeficiente corresponde a cada uno de los dos inmuebles, y sabe que el coeficiente del local es doble que el de la vivienda.
Vamos a resolver el problema de dos formas diferentes. En la primera utilizaremos dos incógnitas. Y en la segunda sólo una incógnita.
Lo planteamos en primer lugar como un sistema de dos ecuaciones.
Si llamamos a las incógnitas x = coeficiente de la vivienda e = coeficiente del local. El sistema quedaría planteado de la siguiente forma
y = 2
x+100 y= 408
Completa los espacios en blanco.
a) Si x = coeficiente de la vivienda, el del local sería 2x. La ecuación queda:
140x+100(2x)=408. | |
b) Si x = coeficiente de la vivienda, el del local sería 2x. Por tanto, la ecuación es: 100x+140(2x)=408. | |
c) Si x = coeficiente del local, el de la vivienda sería 2x. La ecuación sería:
140(2x)+100x=408. | |
d) si x = coeficiente del local, el de la vivienda sería
140( | |
|
a) Los coeficientes son 1,2 del local y 2,4 el de la vivienda.
| |
|
b) 1,1 es el de la vivienda y 2,2 es el coeficiente del local.
| |
|
c) 1,2 es el coeficiente de la vivienda y 2,4 el del local.
| |
|
d) -1,2 el de la vivienda y 2,4 el del local.
|
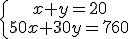 , y resolviéndolo obtendrías que ha vendido 8 pantalones y 12 camisas.
, y resolviéndolo obtendrías que ha vendido 8 pantalones y 12 camisas.
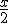 . La ecuación queda:
. La ecuación queda: