1. ¿Qué significa tener otra incógnita?
¿No te ha ocurrido nunca cuando estás organizando algo, como un viaje, que haya gastos fijos y otros no?

Hay muchas situaciones cotidianas en las que entran en contacto distintos elementos, y muchas veces hay varios de ellos que no conocemos. Ya en el primer tema has visto expresiones algebraicas en las que ocurría esto.
Por ejemplo si un familiar nuestro tiene un terrenito en el campo que ocupa 150 m2, en el supuesto de que el terreno sea rectángular, no sabemos exactamente cuánto valen sus lados a partir del valor anterior.
Expresiones de este tipo son las que veremos a continuación.
Nuestro amigo Juan, el de la tienda de moda, ha hecho un pedido de 20 blusas y 17 camisas. Le ha llegado el aviso de envío por un total de 5843,50 € pero no sabe exactamente cuánto le va a costar cada una, porque han quedado en hacerle un precio especial.
Si representamos por "x" el precio al que le pondrán la blusa y por "y" el correspondiente a las camisas, ¿qué expresión corresponde a la situación que relacione el número de blusas y camisas con el coste del pedido?
El hecho de tener más de una incógnita nos va a afectar al número de soluciones que va a tener esa ecuación.
 |
Por ejemplo , si hemos ido con unos amigos al cine y uno de ellos se ha encargado de comprar palomitas y refrescos, puede decirnos que por 3 paquetes iguales de palomitas y 2 refrescos le han cobrado un total de 6 euros, con lo que tendríamos la relación:
3·p + 2·r = 6
pero eso no nos indica cuánto cuesta cada paquete de palomitas y cada refresco, en general podría haber distintas soluciones para esa ecuación.
Recuerda que la solución de una ecuación es el valor (o valores) que sustituido en la incógnita verifica la igualdad.
En el caso de una ecuación con dos incógnitas, cada solución se compone de dos valores, uno para cada una de las variables de la ecuación.
Por ejemplo en la ecuación 4·x - 3·y = 5 una solución serían los valores x=2 e y=1 ya que se verifica que 4·2 - 3·1 = 8 - 3 = 5.
En el caso de los refrescos y las palomitas, podría ser cualquiera de los siguientes valores, según el tamaño de las palomitas y del refresco:
Una ecuación lineal con dos incógnitas "x" e "y" tiene la forma a·x + b·y = c , donde a, b y c son números, por ejemplo la que ya hemos visto:
3·x + 2·y =6
donde hemos sustituido las letras p y r por x e y.
Si tomásemos todos los pares de valores de x e y que cumplen esa ecuación y los representásemos en un eje de coordenadas, nos saldría una línea recta.
Esto puedes comprobarlo gráficamente en la siguiente ventana de Geogebra. Si mueves los deslizadores señalados con a, b y c (debes pulsar sobre el puntito correspondiente y arrastrar) modificarás los coeficientes de la ecuación. También puedes pulsar sobre el punto A y moverlo por la recta, las coordenadas de ese punto son las soluciones de la ecuación.
Utiliza los deslizadores para conseguir que la ecuación de la recta sea 3x+2y=6, es decir coloca a en 3, b en 2 y c en 6 y así obtendrás la ecuación correspondiente a los refrescos y palomitas y comprueba que las soluciones que has visto en la presentación anterior son efectivamente puntos de la recta, es decir mueve el punto A hasta que consigas, por ejemplo, la solución x=1 e y= 1,50.
Quizás pienses que es muy complicado encontrar una solución de una ecuación que tiene infinitas soluciones, y en donde las cosas no están muy bien determinadas, pero es justo lo contrario. En este caso sólo tienes que darle un valor a una de las dos variables y te queda una ecuación lineal de primer grado como las que hemos resuelto en el tema anterior.
Por ejemplo, en el caso de las palomitas y los refrescos, si consideramos que los refrescos valen 1,25 € cada uno, en la ecuación nos quedaría:
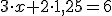
de donde despejando 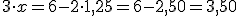
y por tanto cada paquete de palomitas valdría 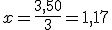 €.
€.
Si consideramos que x representa el número de coches de dos plazas e y el de cinco, la ecuación que relaciona ambas variables es .
ATENCIÓN: Escribe la ecuación en la forma ax+by=c, sin productos ni espacios en blanco. Sustituye a, b y c por los valores correspondientes.
| Para practicar
A lo largo de este tema vamos a incluir varios enlaces a la página Álgebra con Papas. Tanto si quieres comprobar que has asimilado los contenidos, como si necesitas más actividades para practicar, te aconsejamos que le dediques un momento a estos ejercicios.
Habrá veces en las que tendrás que despejar alguna de las variables de una ecuación. Ya vimos en el tema 1 cómo se hacía, pero si quieres practicar haz clic en el siguiente enlace y practica el test n.º 3 y el n.º 4.
|
