2.3. Aunque cambie, es lo mismo.
 |
A Juan y a su familia les gusta mucho ir a los parques de atracciones. El fin de semana pasado asistieron a uno que hay en su ciudad. Fueron 2 adultos y 3 niños por lo que pagaron 104 euros. Si llamamos x al precio en euros de la entrada de un adulto e y al precio de un niño, la ecuación que se plantea es 2x+3y=104.
Se lo pasaron tan bien que el próximo fin de semana piensan ir otra vez acompañados de una familia amiga. En total irán 4 adultos y 6 niños. ¿Cuánto se gastarán en entradas para todos? ¿Cuál será la ecuación planteada ahora?
Como has visto en la evaluación, el valor que hay que pagar para 4 adultos y 6 niños es justo el doble de que que hay que pagar si van 2 adultos y 3 niños. Quiere decir que la ecuación es la misma que teníamos pero multiplicados todos los valores por dos. Las ecuaciones que cumplen esa relación se llaman equivalentes.
Llamaremos ecuaciones equivalentes a aquellas que, siendo distintas, tienen las mismas soluciones. Este concepto se amplía a los sistemas de ecuaciones: dos sistemas serán equivalentes si tienen las mismas soluciones.
Si la ecuación ax+by=c se multiplica o divide por un número distinto de cero, la ecuación resultante es equivalente a la anterior.
Por ejemplo la ecuación 10x+5y=25 es equivalente a la ecuación 2x+y=5 que se ha obtenido dividiendo todos los coeficientes entre 5.
Si en un sistema a una ecuación se le suma o resta otra ecuación distinta, la ecuación obtenida es equivalente a la primera.
Es decir, si tenemos las ecuaciones 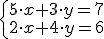 , la ecuación que se obtiene restando a la de arriba la de abajo,
, la ecuación que se obtiene restando a la de arriba la de abajo, 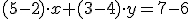 , es equivalente a ambas.
, es equivalente a ambas.

|
En la actividad anterior hemos hallado que por la entrada de un adulto y un niño hay que pagar 43 euros.
También sabemos que una entrada de adulto y dos de niño cuestan 61 €.
Aplica las transformaciones anteriores para saber cuánto cuesta la entrada de un niño.
Juan está pensando alquilar un local para trasladar su tienda al centro comercial. Ha preguntado los precios de los alquileres. En la inmobiliaria le han dicho que el precio depende de dos conceptos, los meses de alquiler y los metros cuadrados del local.
Por 12 meses de alquiler y un local de 200 metros cuadrados piden 18.000 euros. ¿Cuánto pedirán por tres meses de alquiler para un local de 50 metros cuadrados?
|
a) 10.000 euros
| |
|
b) 4.500 euros.
| |
|
c) 3.000 euros.
|
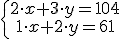 , la de arriba corresponde al gasto realizado por la familia de Juan, y la inferior al de su amiga.
, la de arriba corresponde al gasto realizado por la familia de Juan, y la inferior al de su amiga.
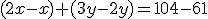
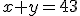 .
.