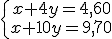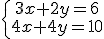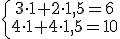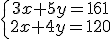2.1. Cuando las ecuaciones vienen en pareja
Siempre se ha dicho que hay cosas que vienen a pares, como los males, los ojos o la Guardia Civil. A eso es lo que vamos a dedicar este apartado.
 |
Ya en el tema anterior vimos ecuaciones donde había un valor desconocido que descubríamos al resolverlas. Aquí nos vamos a encontrar con ecuaciones en las que existen dos incógnitas y para poder resolverlas de forma única, vamos a necesitar dos ecuaciones independientes.
Importante
La expresión general de un sistema de dos ecuaciones lineales con dos incógnitas es el siguiente:
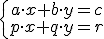donde a, b, c, p, q y r son números y las variables son x e y.
Un ejemplo cualquiera podría ser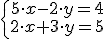 
AV - Reflexión
En el apartado anterior hablamos de una serie de viajes en taxi. Por 4 kilómetros nos cobraron 4,60 € y por 10 kilómetros la tarifa ascendió a 9,70 €.
Si representamos por "x" el precio de la bajada de bandera y por "y" lo que cuesta cada kilómetro, escribe el sistema de dos ecuaciones correspondientes a los datos que te hemos dado.
Importante
La solución de un sistema de ecuaciones está formada por aquellos valores que al sustituirlos en las incógnitas verifican todas y cada una de la ecuaciones del sistema.
Por ejemplo, en el sistema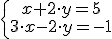 
serían solución los valores x=1 e y=2 ya que se cumplirían las dos ecuaciones.
Ejemplo o ejercicio resuelto
AV - Reflexión
 |
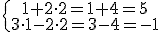
En un teatro cercano a nuestra casa están representando una obra muy interesante. Hay dos tipos de butacas, de patio y de palco, que son más baratas. Un amigo se ha encargado de sacar unas entradas para nuestro grupo. Por tres entradas de patio y cinco de palco ha tenido que pagar 161 euros.
A última hora se han añadido varias personas más al grupo, con lo que hemos tenido que comprar dos butacas de patio y cuatro de palco más pagando 120 euros por ellas.
Plantea un sistema de ecuaciones donde representes por "x" el precio de entrada de la butaca de patio y por "y" la de palco, y que recoja la información que te hemos dado.
AV - Pregunta Verdadero-Falso