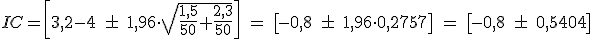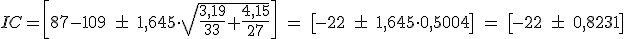3. Comparar la diferencia
 |
| Imagen de Agriculturasp con licencia Creative Commons |
Comparar es algo fundamental en algunos casos. Cuando hacemos investigaciones científicas comparar nos va a servir para ver cuál de las posibilidades de que dispongo es la mejor o la más eficiente.
Podemos ver un ejemplo de esto en los estudios de laboratorio de un determinado medicamento. El mismo medicamento puede ser inoculado a dos series de ratones en distintas condiciones para ver en cual de ellas se obtienen mejores resultados.
Otro ejemplo lo podemos ver en la medida de resultados académicos de dos centros de estudio distintos. Se eligen dos muestras al azar de cada uno de ellos y se les pasa el mismo test para estudiar en cual de los dos los resultados académicos son mejores.
Los políticos, por interés propio, junto con los medios de comunicación encargados de cubrir estas noticias son dados a encargar encuestas a empresas como nuestra TisBet Survey para comparar, frente a unas próximas elecciones, la diferencia de intención de voto entre los dos partidos políticos principales de una ciudad, comunidad autónoma o de todo el país.
En general los estudios irán encaminados a comparar las medias de dos poblaciones referidas a un mismo aspecto. Comparar las medias equivale a hacer un estudio de la diferencia de las mismas, para ver cual de los resultados es mejor. En cualquier caso los estudios se deben hacer escogiendo una muestra de un determinado tamaño de cada población y aplicar las matemáticas para inferir esos resultados a toda la población de la forma más fiable posible.
Obtendremos un intervalo de confianza en el cual se encontrará la diferencia de las medias con una cierta probabilidad que llamaremos nivel de confianza. Generalmente, en los estudios, este nivel de confianza será del 90%, 95% o 99%. Evidentemente, a mayor nivel de confianza mayor será el intervalo obtenido.
En este caso tenemos que comparar las medias de dos poblaciones. Para ello tendremos que usar el estadístico que estudiamos en el tema del Teorema Central del Límite para la diferencia de las medias.
Sean dos poblaciones N(μ1, σ1) y N(μ2, σ2); de cada una de ellas se elige una muestra de tamaños n1 y n2, respectivamente.
Sean 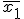 y
y 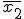 las medias de la primera y de la segunda muestra respectivamente. Para un nivel de significación α, se tiene que
las medias de la primera y de la segunda muestra respectivamente. Para un nivel de significación α, se tiene que
- Si σ1 y σ2 son conocida, el intervalo de confianza viene dado por:
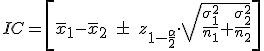
- Si σ1 y σ2 son desconocidas y n1 y n2 son grandes (n1≥30 y n2 ≥30), el intervalo de confianza viene dado por:
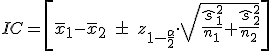
donde 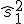 y
y 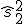 son las cuasivarianzas de cada muestra.
son las cuasivarianzas de cada muestra.
 |
| Imagen de juanpol con licencia Creative Commons |
A nuestras oficinas de TisBet Surbey llegó el siguiente encargo de los laboratorios MIPASTILLA S.A.
En sus laboratorios habían realizado un estudio consistente en la medición, en dos grupos de pacientes, de la cantidad de cierta proteína en sangre en pacientes tras dos tratamientos con distintos medicamentos.
Nos solicitaban que realizásemos una comparativa de los resultados clínicos y para ello nos enviaban los datos del experimento.
El estudio consistía en dos muestras de 50 individuos con los siguientes resultados.
Media(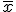 ) ) |
Cuasivarianza (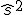 ) ) |
|
| Medicamento 1 |
3,2 | 1,5 |
| Medicamento 2 |
4 | 2,3 |
El encargado de realizar el estudio decide calcular el intervalo de confianza para la diferencia de las medias con un nivel de significación del 95%.
Ayuda a nuestros amigos de TisBet Survey a realizar el estudio ayudándote del intervalo de confianza para la media que acabas de estudiar.
 |
| Imagen de xornalcerto con licencia Creative Commons |
Una planta de tratamiento de aguas residuales, recibe diariamente el agua de dos pequeñas poblaciones próximas, Villalta y Villabajo.
Desde la empresa de tratamiento deciden estudiar, para comparar la calidad de las mismas, la concentración de nitratos disueltos. Para ello se extraen dos muestras al azar y se analiza el contenido de nitratos, obteniéndose los siguientes resultados expresados en mg/l.
Población Villalta:
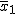 =87 mg/l, σ1=3,19mg/l, n1=33 l
=87 mg/l, σ1=3,19mg/l, n1=33 l
Población Villabajo:
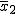 =109 mg/l, σ2=4,15mg/l, n2=27 l
=109 mg/l, σ2=4,15mg/l, n2=27 l
Calcula un intervalo de confianza para la diferencia de las medias con un nivel de significación del 10%.
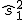 =1,5
=1,5 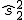 =2,3
=2,3