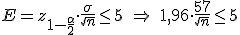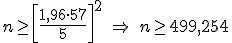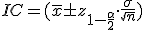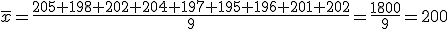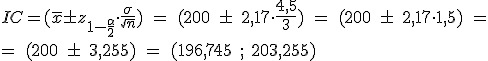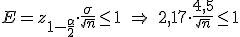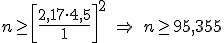2.1. Error y tamaño de la muestra
 |
| Imagen de Daquella manera con licencia Creative Commons |
Los errores aparecen y más cuando estamos realizando cálculos. En este caso, saber cuál es el error que queremos cometer de antemano, nos va a ayudar a decidir cual es el tamaño de la muestra que necesitamos para equivocarnos menos de ese error.
Cuando calculamos un intervalo de confianza para la media estamos indicando un intervalo donde puede que se encuentre la media de la población con una cierta probabilidad, que hemos llamado nivel de confianza.
Es evidente que se comete un error. Puede que la media real de la población esté fuera de ese intervalo. ¿Cuál es el error máximo admisible?
La forma de nuestro intervalo cuando estamos infiriendo la media está centrado en  y le sumamos y restamos una misma cantidad:
y le sumamos y restamos una misma cantidad:
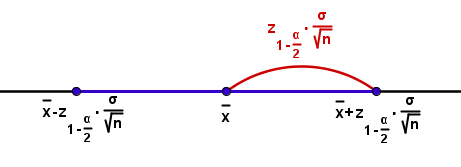 |
El error máximo que se comete, E, es el radio del intervalo centrado en la media y el margen de error es la amplitud del intervalo, 2E.
¡Lo mismo que en el tema anterior, vaya!
El Error máximo admisible en el cálculo de un intervalo de confianza para la media es:
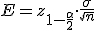
El margen de error admisible es la amplitud del intervalo, 2E.
Si queremos disminuir el error una vez escogido el nivel de significación la única variable que nos queda, en la fórmula anterior del Error máximo admisible, es el tamaño de la muestra. A mayor tamaño muestral el Error disminuirá.
Por lo tanto, si sé cuál es el error máximo que quiero cometer, puedo saber cuál es el tamaño de la muestra que tengo que seleccionar para conseguirlo. Basta con despejar n en la fórmula anterior, con lo que nos queda:
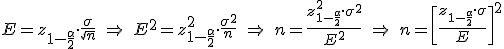
¡Muy parecida a la formula del error máximo para un intervalo de confianza con la proporción!
El tamaño de la muestra para que en el intervalo de confianza se cometa un error prefijado al nivel de significación α es:
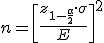
 |
| Imagen de Ignacio Sanz con licencia Creative Commons |
En una comunidad autónoma se está haciendo un estudio sobre el número de días que dura un contrato temporal.
Se sabe que la desviación típica de los contratos es igual a 57 días.
El estudio se quiere hacer con un nivel de confianza del 95%.
Indica el número mínimo de contratos en los que se ha de mirar su duración para que el intervalo que da la duración media de un contrato de ese tipo tenga una amplitud no mayor de 10 días.
 |
| Imagen de Aditza 121 con licencia Creative Commons |
La longitud de los cables de los auriculares que fabrica una empresa es
una variable aleatoria que sigue una ley Normal con desviación típica
4,5 cm. Para estimar la longitud media se han medido los cables de una
muestra aleatoria de 9 auriculares y se han obtenido las siguientes
longitudes, en cm:
205, 198, 202, 204, 197, 195, 196, 201, 202.
a) Halla un intervalo de confianza, al 97%, para la longitud media de los cables.
b) Determina el tamaño mínimo que debe tener una muestra de estos auriculares para que el error de estimación de la longitud media sea inferior a 1 cm, con el mismo nivel de confianza del apartado anterior.
 |
| Imagen de William Sealy Gosset de Wikimedia Commons |
William Sealy Gosset (11 de junio de 1876 – 16 de octubre de 1937) fue un estadístico, mejor conocido por su sobrenombre literario Student. Asistió a la famosa escuela privada Winchester College, antes de estudiar química y matemáticas en el New College de Oxford. Tras graduarse en 1899, se incorporó a las destilerías Guinness en Dublín.
Guinness era un negocio agroquímico progresista y Gosset podría aplicar sus conocimientos estadísticos tanto a la destilería como a la granja (para seleccionar las mejores variedades de cebada).
Para evitar el espionaje industrial, Guinness había prohibido a sus empleados la publicación de artículos independientemente de la información que contuviesen.
Esto significaba que Gosset no podía publicar su trabajo usando su propio nombre. De ahí el uso de su seudónimo Student en sus publicaciones, para evitar que su empleador lo detectara. Por tanto, su logro más famoso se conoce ahora como la distribución t de Student, que de otra manera hubiera sido la distribución t de Gosset.
La distribución t de Student se usa como distribución del estimador muestral de la media cuando la muestra tiene muy pocos individuos, es decir, n es muy pequeño.