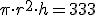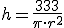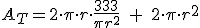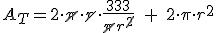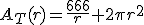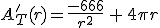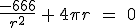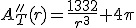2.1. Vamos a la cervecita, la coca-cola, la fanta,...
 |
| Imagen de martiniko bajo licencia Creative Commons |
Seguro que más de una vez en la playa has visto a los simpáticos vendedores de refrescos dando una vuelta y otra intentando vender algo bajo el sofocante calor veraniego. ¡Qué no! Bueno, es igual, tampoco pasa nada. Llégate si eso un momento al frigorífico y cógete alguna lata de refresco. ¿Que tampoco tienes latas de refrescos? Pues nada, cuando vayas al súper piensa sobre esto. ¿Por qué todas las latas, sean de la marca que sean y tengan el producto que tengan de 33 cl son iguales?
No, no es ninguna tontería. Podrían ser unas más alargadas, otras más anchas, y seguir teniendo el tercio de litro, pero no. Todas son iguales. Pero,... ¿lo harán bien? ¿Es ese el mejor diseño?
Observa la siguiente escena. En azul, tenemos la lata de forma cilíndrica de un tercio de litro, que equivale a 333 cm3 (1 litro = 1000 cm3).
A la izquierda, tenemos el desarrollo plano de la lata, como si cogiéramos una tijera, cortáramos y extendiéramos sobre la mesa el metal con el que está hecha la lata. Saldrían los dos círculos de las tapas y el rectángulo de la pared lateral. Moviendo el punto verde, puedes variar la forma de la lata estrechando o ensanchando ese rectángulo, pero fíjate que el volumen siempre es constante.
Claro al fabricante de latas, le interesa que el coste de cada lata sea mínimo, y el coste se traduce en la cantidad de material que hace falta para construir la lata. Ese material no es mi más ni menos que el área total del cilindro, es decir, la suma del área lateral y el de las dos tapas.
Mueve el punto verde y observa cómo varía el área y por tanto el material necesario según sea la forma de la lata. ¿Cuándo se obtiene el mínimo y por tanto la mejor opción?
Pero, ¿por qué ocurre con esas medidas?
Applet geogebra modificado del original de Manuel Sada bajo licencia Creative Commons.
Y si ahora le quitamos la tapa de arriba, o sea, como si hiciéramos un lapicero, ¿cuáles serían las mejores medidas para la lata?
Empezamos por la función. La función a la que ahora habría que encontrarle el mínimo sería:
|
La misma, pues nada cambia.
| |
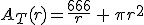
| |
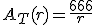
| |
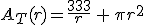
|
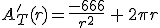
| |
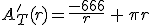
| |
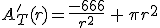
| |
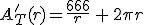
|
|
r = 3,7 cm y por tanto h= 7,5 cm.
| |
|
r = 3,14 cm y por tanto h = 10 cm
| |
|
r = 4,7 cm y h = 4,8 cm.
|
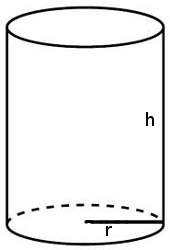 Lo que queremos que sea mínimo es el área total de la lata, por tanto, vamos a empezar construyendo esa área.
Lo que queremos que sea mínimo es el área total de la lata, por tanto, vamos a empezar construyendo esa área.