2.2. Cajón de sastre
 |
| Imagen de seiho bajo licencia Creative Commons |
Ahora te vamos a plantear un ejemplo en el que hay que buscar un máximo.
Imagínate que tienes un cartón cuadrado de 6 unidades de lado (ponle tú las unidades, cm, dm, m, lo que quieras) y quieres construir una caja, sin tapadera para meter los juguetes de los niños, las herramientas, ropa,... , o por ejemplo en el caso de Martín y su hermana, para guardar semillas. ¿Cómo hacer el corte para que el volumen sea el mayor posible?
Observa la siguiente escena, Tenemos arriba el cartón extendido de 6 x 6. El botón verde indica por donde cortaríamos para levantar la pared de la caja. Así en un tono más oscuro aparece la cartulina que usaríamos para elaborar la caja y en un tono más claro el cartón que desperdiciaríamos. Muévelo y observa que la forma de la caja (abajo) va variando y por tanto varía también el volumen de la misma. Lo suyo es que en la caja quepa lo máximo posible ¿verdad? Así que tenemos que buscar qué altura le damos a la caja para confeccionarla de la mejor manera posible. ¿Cuál debe ser? Ojo, recuerda que el volumen de estas figuras (prismas) se calculan multiplicando el área de la base por la altura.
Si quieres cambiar las medidas del largo y ancho del cartón puedes hacerlo moviendo los puntos amarillos, aunque vamos a ver como resolverlo con esas medidas de 6 x 6.
Applet modificado del original de Manuel Sada bajo licencia Creative Commons.
Ve pulsando sobre la presentación para ir avanzando sobre ella y ver cómo obtener la solución:
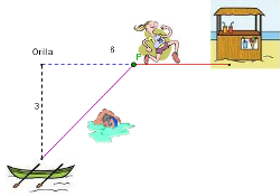 ¿Recuerdas a nuestro nadador del primer punto del tema?
¿Recuerdas a nuestro nadador del primer punto del tema?
Teníamos a Martín en una barca y quería llegar a un chiringuito que se encontraba a 6 km del punto más próximo de la playa que se encontraba a 3. La cuestión era en qué punto de la playa debía desembarcar teniendo en cuenta que nadaba a 3 km/h y podía correr a 10 km/h.
Esta cuestión se resuelve de forma similar; planteando una función a la que buscarle el mínimo, en este caso habrá que buscar la fórmula de la función tiempo, derivar e igualar a cero.
La solución que sale, es que debe arribar en la playa en el punto que se encuentra a 5,06 km del chiringuito.
Si quieres ver la solución con todos los detalles, sigue este enlace.
En esta presentación, tienes unos cuantos ejemplos más resueltos sobre optimización de funciones por si quieres seguir practicando:
