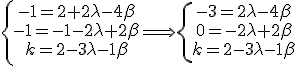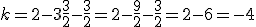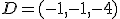2.3. El transporte más utilizado
Dado un punto 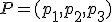 y dos vectores
y dos vectores 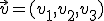 y
y 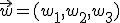 si tenemos el plano
si tenemos el plano 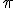 , plano que pasa por el punto
, plano que pasa por el punto 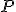 y cuyos vectores directores son
y cuyos vectores directores son 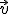 y
y 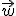 , si
, si 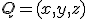 es un punto del plano, entonces los vectores
es un punto del plano, entonces los vectores 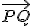 ,
, 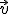 y
y 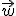 son vectores linealmente dependientes, es decir, el determinante formado por ellos tres es cero.
son vectores linealmente dependientes, es decir, el determinante formado por ellos tres es cero.
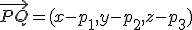
Luego
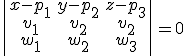 Desarrollando el determinante por menores de la primera fila:
Desarrollando el determinante por menores de la primera fila:
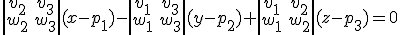 si llamamos
si llamamos 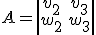 ,
, 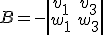 y
y 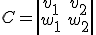
La ecuación nos quedaría: 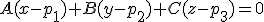 si desarrollamos tenemos que
si desarrollamos tenemos que 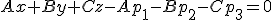 , pero
, pero 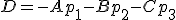 es un número,
es un número,
luego nos queda
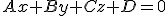
Esta es la ecuación implícita del plano. Es la forma de ecuación del plano más utilizada, por eso a veces se le llama ecuación general del plano.
Además, se cumple que el vector 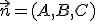 es un vector perpendicular al plano que se denomina vector normal del plano. En la escena de abajo te mostramos un plano que pasa por el punto
es un vector perpendicular al plano que se denomina vector normal del plano. En la escena de abajo te mostramos un plano que pasa por el punto 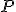 y que tiene por vectores directores
y que tiene por vectores directores 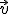 y
y 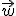 . En la escena también aparece el vector normal
. En la escena también aparece el vector normal 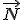 . Mueve los elementos de la escena y comprueba que el vector normal siempre es perpendicular a los vectores directores y, por tanto al plano. De esta forma ya conoces la forma de obtener un vector perpendicular a dos vectores dados.
. Mueve los elementos de la escena y comprueba que el vector normal siempre es perpendicular a los vectores directores y, por tanto al plano. De esta forma ya conoces la forma de obtener un vector perpendicular a dos vectores dados.
Instrucciones:
- Arrastra el ratón para rotar la figura.
- Arrastra los puntos al final de las flechas así como el origen (para trasladar v y w al plano)
- Shift + arrastre vertical = zoom
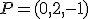 y tiene como vectores directores
y tiene como vectores directores 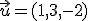 y
y 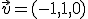
Instrucciones:
- Arrastra el ratón para rotar la figura.
- Arrastra los puntos con el ratón, así como la base de N en el plano. Observa que el vector normal siempre es perpendicular al plano.
- Shift + arrastre vertical = zoom
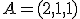 ,
, 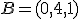 y
y 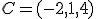 .
.
 |
| Industria siderúrgica. Imagen obtenida del banco de imágenes del ITE. |
En
una empresa siderúrgica pretenden trasladar una plancha muy pesada. El
diseñador encargado del trasporte ha dibujado la plancha en un plano
cuya ecuación implícita es: 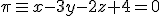 y uno delos puntos que va a sujetar la plancha se encuentra en el punto
y uno delos puntos que va a sujetar la plancha se encuentra en el punto 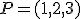 .
.
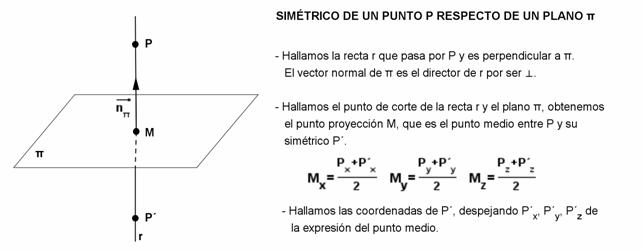
El otro punto que debe sujetar la plancha se debe situar en el punto simétrico a 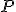 respecto al plano
respecto al plano 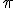 . Calcula las coordenadas de ese punto.
. Calcula las coordenadas de ese punto.
Instrucciones:
- Arrastre el mouse para rotar la figura.
- Arrastre el punto en P y también la base del vector N para trasladarlo al plano.
- Shift + arrastre vertical = zoom
|
|
En
un hospital especializado en operaciones cerebrales han realizado un
corte trasversal del cráneo de un paciente en el que han identificado 3
nódulos peligrosos situados en los puntos: 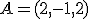 ,
, 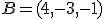 y
y 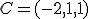
En la operación, el equipo médico debe colocar un emisor eléctrico en otro punto del que conocen que sus dos primeras coordenadas son -1 y -1, pero además, este punto debe estar en el mismo plano en el que se encuentran los puntos 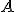 ,
, 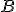 y
y 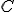 . Calcula las coordenadas exactas en las que deben colocar el emisor eléctrico.
. Calcula las coordenadas exactas en las que deben colocar el emisor eléctrico.
Como ya conoces, una de las ecuaciones que determina una recta es la ecuación implícita que tiene la siguiente forma:
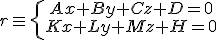
En realidad, la primera ecuación corresponde a un plano
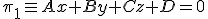 y la segunda a otro plano
y la segunda a otro plano 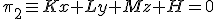 por lo que la recta viene determinada por los puntos que cumplen las dos ecuaciones a la vez, es decir, los puntos que están en los dos planos o, lo que es lo mismo, los puntos de corte de los dos planos.
por lo que la recta viene determinada por los puntos que cumplen las dos ecuaciones a la vez, es decir, los puntos que están en los dos planos o, lo que es lo mismo, los puntos de corte de los dos planos.
En la siguiente animación puedes ver lo que te indicamos. Además, observa que el vector director de la recta que resulta al cortar los dos planos es perpendicular a los vectores normales de los planos
Instrucciones:
- Arrastra el ratón para rotar la figura.
- Tecla S + movimiento vertical del mouse = zoom
- Observa que los dos planos se cortan en una recta
- Observa que los vectores normales de los planos son perpendiculares a la recta en la que se cortan
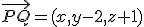 , y los vectores directores del mismo
, y los vectores directores del mismo 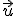 y
y 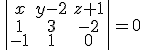
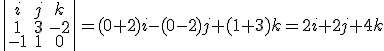
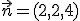 nos determinan los coeficientes
nos determinan los coeficientes 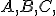 de la ecuación implícita del mismo, el coeficiente
de la ecuación implícita del mismo, el coeficiente 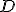 lo hallamos a partir del punto
lo hallamos a partir del punto 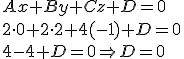
 . En este caso, esta recta pasa por el punto
. En este caso, esta recta pasa por el punto 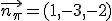 . Así, la ecuación paramétrica es:
. Así, la ecuación paramétrica es:
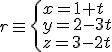
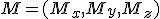 es un punto de la recta anterior, por tanto sus coordenadas deben cumplir la ecuación de la recta.
es un punto de la recta anterior, por tanto sus coordenadas deben cumplir la ecuación de la recta.
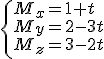
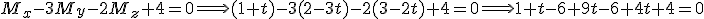
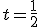
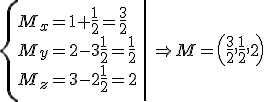
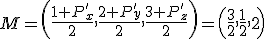
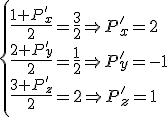
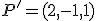
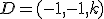 al punto en el que se debería colocar el emisor eléctrico. Lo primero que vamos a hacer es calcular el plano que forman los tres primeros puntos. Para ello necesitamos un punto y dos vectores directores. Los vectores directores van a ser:
al punto en el que se debería colocar el emisor eléctrico. Lo primero que vamos a hacer es calcular el plano que forman los tres primeros puntos. Para ello necesitamos un punto y dos vectores directores. Los vectores directores van a ser:
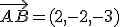 y
y 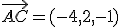 . Vamos a utilizar como punto
. Vamos a utilizar como punto 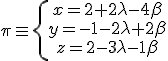
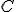 , por tanto el punto
, por tanto el punto 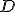 debe cumplir las ecuaciones del plano
debe cumplir las ecuaciones del plano