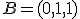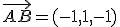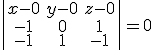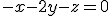3. Especial selectividad
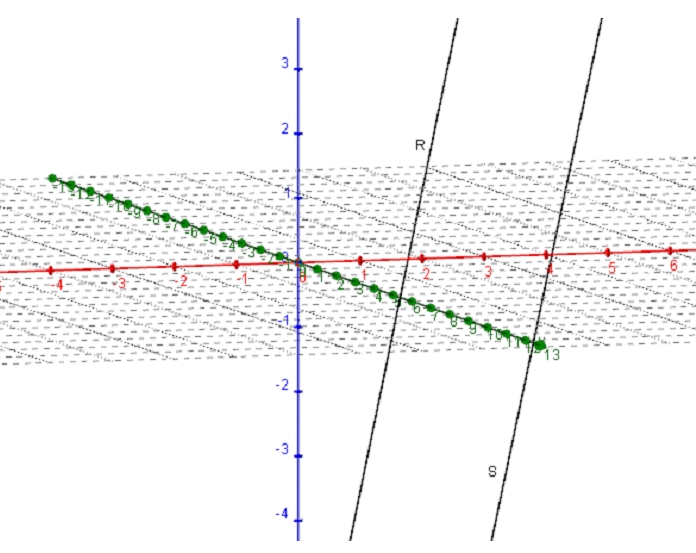
Halla la ecuación del plano 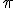 que contiene a la recta
que contiene a la recta  y es paralelo a la recta
y es paralelo a la recta  , siendo
, siendo
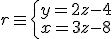 y
y 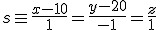
Determina un plano que, pasando por el origen de coordenadas sea paralelo a la recta de ecuación 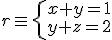 y también que sea paralelo a la recta que pasa por los puntos de coordenadas
y también que sea paralelo a la recta que pasa por los puntos de coordenadas 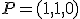 y
y 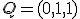
 y
y 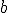 para que los puntos de coordenadas
para que los puntos de coordenadas 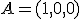 ,
, 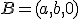 ,
, 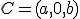 y
y 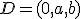 estén en un plano.
estén en un plano.
Determina la ecuación de la recta  que pasa por el punto
que pasa por el punto 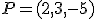 y es paralela a la recta
y es paralela a la recta
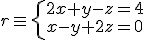
 y
y 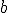 para que el punto
para que el punto 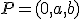 esté en el plano determinado por los puntos
esté en el plano determinado por los puntos 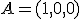 ,
, 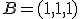 y
y 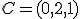 .
.
a) Determina la recta que pasa por el punto (1,1,1) y es perpendicular al plano de ecuación 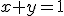
b) Calcula el punto de corte entre la recta calculada y el plano dado.
Halla el plano que contiene a la recta  y es paralelo a la recta
y es paralelo a la recta  sabiendo que:
sabiendo que:
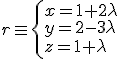 y que
y que 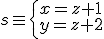
a) Determina el plano que pasa por el punto de coordenadas (1,1,1) y corta perpendicularmente a la recta de ecuación
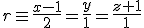
b) Calcula el punto donde se cortan la recta y el plano

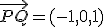
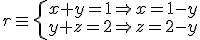
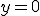 obtenemos el puntos
obtenemos el puntos 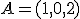 .
.
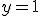 obtenemos el punto
obtenemos el punto