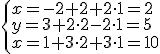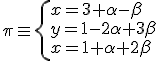2.2. Cómo llegar paso a paso
Dado un punto 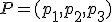 y dos vectores
y dos vectores 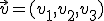 y
y 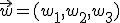 sabemos que la ecución vectorial del plano que pasa por el punto y tiene esos dos vectores directores es
sabemos que la ecución vectorial del plano que pasa por el punto y tiene esos dos vectores directores es
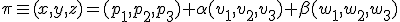
Igualando coordenada a coordenada tenemos que:
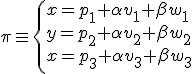
A esta ecuación se le llama ecuación paramétrica del plano. En la siguiente imagen interactiva puedes ver como se obtienen los puntos del plano a través de uno de sus puntos y la combinación lineal de sus vectores directores.
Instrucciones:
- Arrastra el ratón para rotar la figura.
- Arrastra el punto rojo y observa como se va obteniendo a partir de la ecuación paramétrica del plano.
- Shift + arrastre vertical = zoom
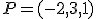 y tienen por vectores directores los vectores
y tienen por vectores directores los vectores 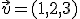 y
y 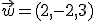 . Calcula otro punto cualquiera del plano y represéntalo utilizando la ventana interactiva que hay más abajo.
. Calcula otro punto cualquiera del plano y represéntalo utilizando la ventana interactiva que hay más abajo.
| Plano determinado por un punto y dos vectores. Animación realizada por Jesús Fernández Martín de los Santos |
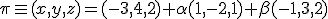 Calcula la ecuación paramétrica del plano paralelo al anterior y que pase por el punto
Calcula la ecuación paramétrica del plano paralelo al anterior y que pase por el punto 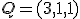 . Dibuja ambos planos en la escena interactiva que está más arriba y comprueba que son paralelos.
. Dibuja ambos planos en la escena interactiva que está más arriba y comprueba que son paralelos.
 |
En algunos casos estamos acostumbrados a utilizar materiales en 2 dimensiones, en el plano, que a pesar de que el mundo que nos redoa es un espacio en tres dimensiones, nos cuesta más utilizarlas en esas tres dimensiones. Piensa en alguna de ella. Nosotros te vamos a proponer una lúdica. Suponemos que conoces el famos juego llamada Tetris. Se han hecho muchas versiones de este juego, pero todas ellas en el plano, en dos dimensiones. ¿Te atreverías a juagar al tetris con piezas en tres dimensiones? A la izquierda de este texto puedes ver una imagen de cómo sería. Pulsa sobre ella y podrás jugar en tres dimensiones.
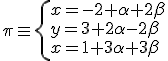
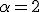 y
y 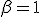 por ejemplo. Entonces tenemos:
por ejemplo. Entonces tenemos: