3. Miss función radical
 |
| 12. Imagen de cassimano bajo licencia Creative Commons |
Estas funciones, también llamadas irracionales, son las que en su expresión tienen algún radical, es decir, alguna raíz. La más simple, es evidentemente esta:
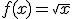
Si queremos ver cómo es la gráfica, basta con que hagamos una pequeña tabla y veamos cómo va evolucionando. Ahora bien, puesto que en los números reales, las raíces negativas no existen, a "x" habrá que darle valores mayores o iguales que cero, es decir,
Dom(f) = [0 , + ∞)
Por otro lado, si recuerdas, la raíz cuadrada tiene dos resultados; uno positivo y otro negativo (por ejemplo 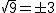 ), pero para que tengamos una función hemos de quedarnos con un solo resultado; el positivo.
), pero para que tengamos una función hemos de quedarnos con un solo resultado; el positivo.
Ahora sí, podemos hacer la tabla:
| x |
0 | 1 | 4 | 6 | 8 | 9 | 10 | 12 |
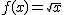 |
0 | 1 |
2 |
2,4 |
2,8 |
3 |
3,2 |
3,5 |
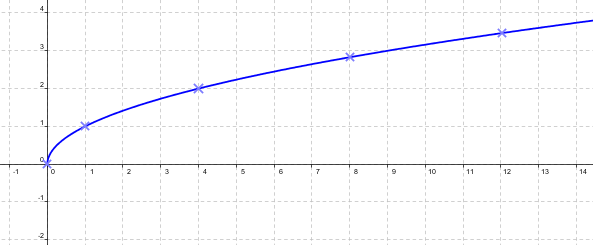
Y representando y uniendo los puntos tenemos la gráfica:
 |
En la siguiente escena, representamos la función 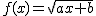 . Modifica los controles de "a" y "b" y observa lo que ocurre.
. Modifica los controles de "a" y "b" y observa lo que ocurre.
Applet Descartes de José María Lobo Rodríguez de Fregenal de la Sierra bajo licencia Creative Commons
Contesta a las siguientes cuestiones a partir de la escena anterior:
- Si multiplicamos x por un número positivo (a>0), ¿la función es creciente o decreciente?
- ¿Qué ocurre si a "b" le damos un valor positivo? ¿Y si es negativo?
- Si a = -1 y b = 3, ¿cuál es el dominio de la función? ¿La función crece o decrece?
- ¿Puede la "x" alguna vez tomar valores negativos? ¿Y la función f(x)?