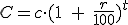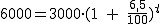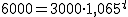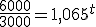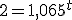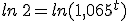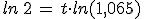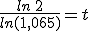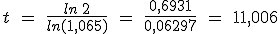2.2 ¡Hasta en ecuaciones!
Ejemplo o ejercicio resuelto
En este apartado, vamos a ver cómo se aplican los logaritmos en la resolución de ecuaciones.
 |
| 10. Imagen de Fran Villena (villano) bajo licencia Creative Commons |
Isidoro, es agricultor y como este año la cosecha de la aceituna ha ido muy bien, ha obtenido grandes beneficios por la explotación de su terreno. Así que, va a depositar un dinero en una entidad financiera, pero para asesorase acude a nuestro amigo Evaristo. Evaristo le cuenta que la mejor opción es el banco JKL-MOOM, que le ofrece un depósito al 6,5% de interés anual.
Isidoro, que quiere comprarse una nueva máquina para arar la tierra, le pregunta a Evaristo: bien, y si deposito 3000 €, ¿cuánto tiempo tendré que esperar para que se me duplique y tenga 6000 € para comprar la máquina?
Evaristo, sin excesivos problemas, le contesta que tendrá que esperar un poquito y que mejor que vaya echando otras cuentas para comprarse la máquina porque con esas no se la compra.
Vamos a ver cómo calcula esto Evaristo.
AV - Actividad de Espacios en Blanco
Redondea el resultado a 3 cifras decimales.
Primero deja solo el factor con x y después toma logaritmo.
2x = 12 → x=
0,4x = 4 → x=
10·3x = 154 → x=
2·5x -10 = 425 → x=
Para saber más
Estas ecuaciones que hemos resuelto, se llaman ecuaciones exponenciales, pues la incógnita aparece en el exponente.
Aquí hemos visto las más simples, las que tienen una única "x" y por tanto se puede despejar con ayuda de los logaritmos, pero esto no siempre es así. Hay ecuaciones exponenciales con la "x" en varios sitios. En el siguiente enlace tienes distintos tipos de ecuaciones exponenciales, la técnica para resolverlas y ejercicios para practicar.
Existen también ecuaciones logarítmicas. En éstas, la incógnita aparece dentro de uno o varios logaritmos. La técnica consiste en agrupar todos los términos de cada lado de la igualdad en un solo logaritmo, aplicando las propiedades de éstos, con la misma base a ambos lados. Conseguido esto, podemos eliminar los logaritmos y quedarnos con una ecuación de las que ya sabemos resolver.
En el siguiente enlace puedes ver más sobre ecuaciones logarítmicas y cómo resolverlas y en el siguiente vídeo puedes ver una un tanto compleja resuelta.