1. Miss función exponencial
 |
| 2. Imagen de Daquella manera bajo licencia Creative Commons. |
¿Recuerdas esta fórmula?
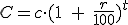
La vimos en la primera unidad; en el tema 3, y era la fórmula del interés compuesto, ¿te acuerdas ahora?
c indicaba la cantidad que se aportaba, r el interés, t el tiempo (en años) y C el capital final obtenido.
Pues bien, vamos a suponer que invertimos 1 euro al 60% de interés y queremos determinar el capital que obtenemos según el tiempo que lo tengamos depositado. Entonces, nuestra fórmula se habrá convertido en:
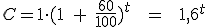
Así, podríamos definir una función que me da el dinero obtenido en función del tiempo que dura la inversión. La variable independiente "x" sería el tiempo y la variable dependiente "y", el dinero obtenido, y la relación sería:
f(x) = 1,6x
Como puedes observar, esta función tiene una forma totalmente distinta de las que hemos visto, pues ahora la variable "x", aparece en el exponente.
Como hicimos con las otras funciones, vamos a hacer una tabla de valores para ver cómo sería la gráfica de esta función:
| X tiempo (años) |
0 |
1 | 2 | 4 | 5 | 10 | 15 |
| Y Capital (€) |
1 | 1,6 | 2,56 |
6,55 |
10,49 | 109,95 |
1152,92 |
A simple vista, observamos que la función va creciendo, pero de una manera ni mucho menos proporcional, pues conforme van pasando los años, nuestro capital se dispara.
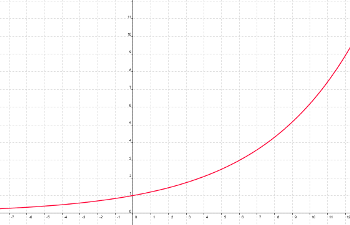
La gráfica quedaría más o menos así:

Como puedes ver únicamente están representados los primeros puntos, y es que para representar los siguientes tenemos que modificar escalas y zoom. Puedes pensar que esto se parece a lo de las parábolas, pero con los 7 puntos vas a ver que no es así, que se dispara hacia arriba mucho más rápido.
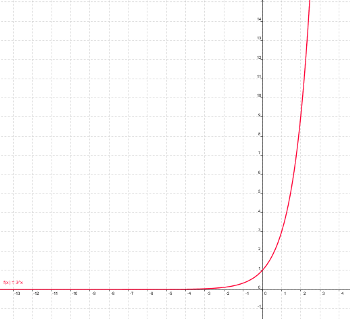
La gráfica de todos los puntos calculados sería así:

Fíjate que para visualizar el valor que le correspondería a los 10 o a los 15 años, apenas se distinguen los valores de los primeros años, y además, puedes observar, que en absoluto se parecen esos puntos a los de una parábola.
Si uniéramos todos los puntos y le diéramos valores decimales al tiempo, la gráfica completa de la función sería:
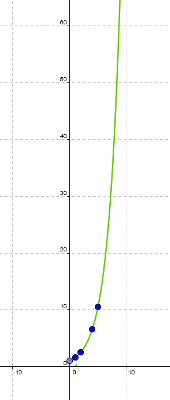
¿Y valores negativos?, ¿podremos darle a "x" valores negativos?
Una potencia con exponente negativo es equivalente a una fracción con numerador 1 y denominador la misma potencia con exponente positivo.
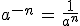
Así, por ejemplo, 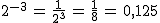
Bien, pues vamos entonces a completar la gráfica de la función f(x) = 1,6x, haciendo una tabla con algunos valores negativos.
| x | -1 | -2 | -5 | -10 |
| f(x)=1,6x |
0,625 |
0,391 | 0,095 | 0,009 |
Si representamos gráficamente los puntos obtenidos en ambas tablas obtenemos algo así:
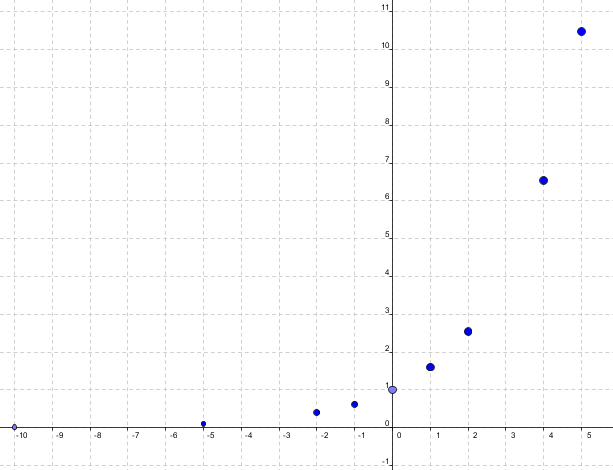
Y si los unimos, obtenemos la gráfica de la función f(x) = 1,6x
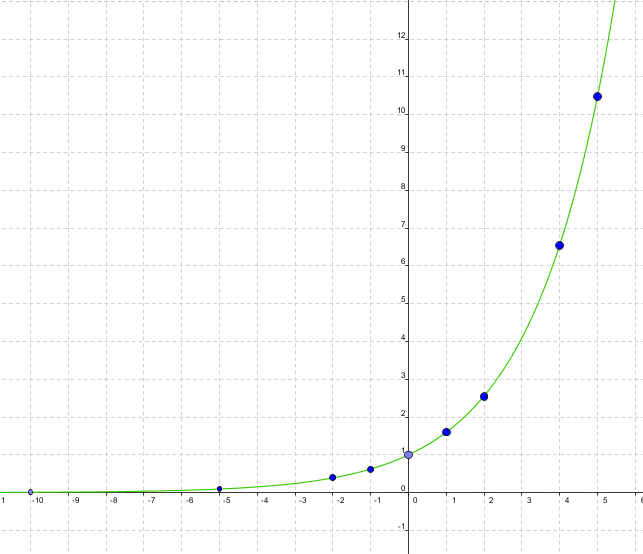
Una función exponencial es una función de la forma:
f(x) = ax,
donde "a" es un número real que en el siguiente apartado veremos las condiciones que tiene que cumplir.
La gráfica de estas funciones tiene siempre una forma similar a la gráfica de arriba.
Cógete calculadora, lápiz y papel y haz la gráfica de las funciones f(x) = 3x y g(x) = 1,2x, elaborando una tabla de valores similar a la que hemos hecho anteriormente.
Las funciones exponenciales aparecen en numerosos procesos de la naturaleza donde se produce un crecimiento o decrecimiento rápido. Por ejemplo, algunas bacterias se reproducen por bipartición, pues bien, el número de bacterias en función del tiempo obedecen a una función exponencial.
El siguiente vídeo muestra cómo va aumentando rápidamente el número de bacterias:
Y he aquí otro ejemplo de crecimiento exponencial; ahora con pulpos: