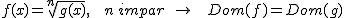3.1 Par o impar
 |
| 13. Imagen de Emi bajo licencia Creative Commons |
En la escena del apartado anterior has visto que la gráfica de la función se desplaza si se multiplica la "x" de dentro de la raíz cuadrada o si se le suma una cantidad. Y es que, como ya hemos comentado, la cifra que quede dentro de la raíz tiene que ser positiva.
En las siguientes escenas puedes ver de manera clara que el dominio de estas funciones radicales coincide con la zona donde la función de dentro de la raíz es positiva:
Applets Descartes de Federico Bertólez Ruiz bajo licencia Creative Commons.
| Y = X - 1 | f(x) = raíz(x-1) |
En las dos siguientes escenas tenemos en primer lugar la función y=ax2 + bx +c, y a la derecha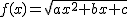 
.
Nuevamente puedes ver que sean los valores de a, b y c los que sean, la función f(x) existe cuando el argumento de dentro es positivo.
Importante
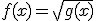
el dominio de la función es el conjunto de valores donde g(x) es mayor o igual que cero:
AV - Reflexión
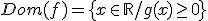
Determina el dominio de las siguientes funciones:
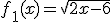
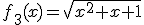
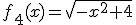
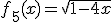
Vamos ahora a ver lo que ocurre con la raíz cúbica.
En las siguientes escenas hemos representado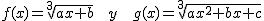 
. Manipula en ambos casos los controles de los coeficientes y observa lo que ocurre.
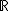, haya dentro de la raíz cúbica lo que haya; y es que, las raíces cúbicas de números negativos sí existen. Un número negativo elevado a 3 da como resultado otro número negativo.
Importante
Para determinar el dominio de una función con raíz cuadrada (o cualquiera de índice par), hemos de ver dónde lo de dentro de la raíz (radicando) es positivo. Luego la función radical existe en los puntos del dominio del radicando donde éste es positivo:
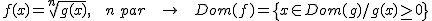
En una raíz de índice impar no importa el signo del radicando. En principio, el dominio está formado por todos los números reales salvo que la función de dentro aporte alguna restricción. Es decir, el dominio de la función radical coincide con el dominio del radicando:
