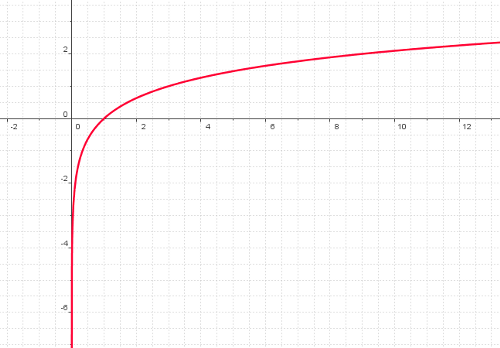
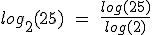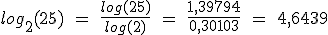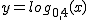2.1 Un logaritmo con nombre y apellidos
Ya sabemos que el logaritmo es una operación matemática que existe cuando la base es mayor que cero y distinta de 1, pero hay dos que son especialmente interesantes. Uno es el logaritmo decimal y otro el logaritmo neperiano.
Si te coges cualquier calculadora científica, verás que hay dos teclas en las que en una aparece "log" y en otra "ln". Pues bien, estas son las teclas que sirven para hacer los logaritmos decimales y los logaritmos neperianos.
El logaritmo decimal es el logaritmo en base 10 y su uso es muy común por la facilidad del cálculo. Observa que al hacer un logaritmo, estamos buscando el valor del exponente, y las potencias de base 10 son las más fáciles de calcular; 1, 10, 100, 1000,... ó, 0,1, 0,01, 0,001,...
Un logaritmo, salvo que sea exacto, es decir, que sea una potencia entera de la base, dará como resultado un número irracional, y si la base de este logaritmo es 10, podemos buscar por aproximaciones fácilmente el valor de éste.
Es tan común el uso de este logaritmo, que por defecto, cuando no se indica base ninguna en un logaritmo, nos estamos refiriendo al logaritmo en base 10:
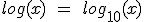
El otro logaritmo, el logaritmo neperiano, es un poco más especial. La base de ese logaritmo es un número irracional cuyo valor es 2,7182818...., y que se llama "e". Sí, e; número e. Esto que en principio parece nada práctico, resulta todo lo contrario como verás el curso próximo, pues la función exponencial más simple es f(x) = ex y el logaritmo más básico es el logaritmo neperiano.
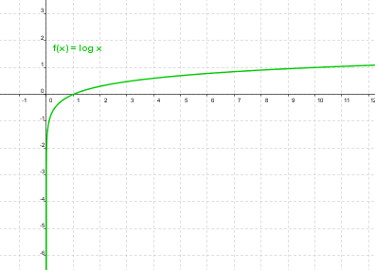
A continuación, tienes las gráficas de ambas funciones:
 |
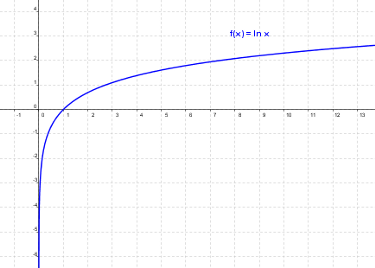 |
| f(x)=log x |
g(x)= ln x |
El número e
Este número e = 2,71828182..., no surge por casualidad. Este valor, es al que se acerca la expresión 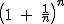 cuando a "n" le vamos dando valores muy grandes, aunque también existen otras expresiones que dan lugar al número e.
cuando a "n" le vamos dando valores muy grandes, aunque también existen otras expresiones que dan lugar al número e.
Fíjate en el siguiente vídeo cómo se puede obtener también, aunque habría que dividir por 100, los 100 pesos, el resultado que da el vídeo.
El número e, base de los logaritmos naturales o neperianos, es sin duda el número más importante del campo del cálculo.
En el próximo curso verás una operación matemática con funciones de importancia crucial; la derivada de una función. Y justamente, la función exponencial f(x) = ex, es la única que al derivarse se queda igual, es decir, es la única función que coincide con su derivada.
Debido a esto, esta función exponencial suele aparecer en el resultado de ecuaciones diferenciales sencillas. Como consecuencia de esto, describe el comportamiento de acontecimientos físicos regidos por ecuaciones diferenciales sencillas, como pueden ser la velocidad de vaciado de un depósito de agua, el giro de una veleta frente a una ráfaga de viento, el movimiento del sistema de amortiguación de un automóvil o el cimbreo de un edificio metálico en caso de terremoto. Si nos fijamos con atención, en todos estos ejemplos podemos encontrar el número e. De la misma manera, aparece en muchos otros campos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos (descarga de un condensador, la amplificación de corrientes en transistores BJT, etc.), biológicos (crecimiento de células, etc.), químicos (concentración de iones, periodos de semidesintegración, etc.), y muchos más.
En el siguiente enlace, puedes saber mucho más sobre el número e, su descubrimiento y utilidades.
Por tanto, ya sabemos que con ayuda de la calculadora podemos calcular un logaritmo en base 10 o un logaritmo neperiano. Pero, ¿y todos los demás?
Por ejemplo, ¿cuánto vale 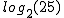 ?
?
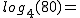
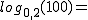
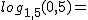
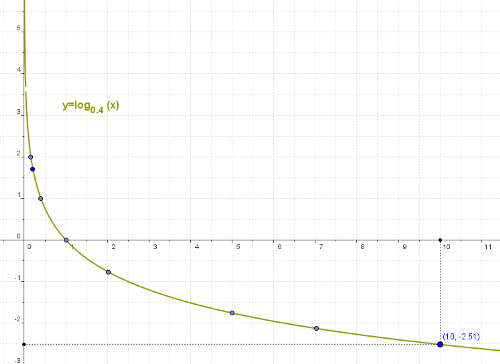
Ahora que ya sabemos calcular cualquier logaritmo, sí que podemos hacer la gráfica de una función logaritmo, sabiendo cómo ha de ser la forma, basta con calcular una tabla de valores para ajustar el gráfico.
Por ejemplo, vamos a representar gráficamente, la función 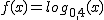 .
.
Ahora te toca a ti. Coge lápiz, papel y calculadora y siguiendo el mismo procedimiento representa gráficamente la función:
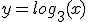
 |
| 9. Imagen de enpasedecentrale bajo licencia Creative Commons |
Otro fenómeno natural donde se usan los logaritmos es en los terremotos. Cada día ocurren en el mundo muchos aunque solo algunos de vez en cuando provocan destrucción e incluso muertes.
La escala que ha sido desarrollada para medir los terremotos se le conoce como la escala Richter que lleva el nombre del sismólogo americano Charles Richter (1900-1985). La fuerza de un terremoto medida por la escala Richter está dada por la expresión 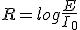 , donde E es la
, donde E es la
intensidad de las vibraciones del terremoto medido e I0 es la intensidad de la unidad de un terremoto estándar. Esta unidad estándar es medida por un instrumento conocido como un sismógrafo, el cual detecta las vibraciones en la corteza terrestre.
Un terremoto de 3 unidades en la escala Richter, prácticamente no es sentido por la población, en la Sierra de Cádiz (Olvera, Algodonales, Coripe, Morón,...) los suele haber cada cierto tiempo, pero uno de 7,2 ocasionó casi 2000 muertos en Japón en el año 95. ¿Puede esta pequeña diferencia variar tanto la intensidad de uno a otro?
Pues sí, y es que teniendo en cuenta que el logaritmo es el valor del exponente y que estamos en base 10, esa diferencia de 4,2 unidades indica que el terremoto de Japón es 104,2 veces más intenso que el de 3 unidades, o sea, 15850 veces más potente.
Debido a que la escala Richter es una escala logarítmica, las diferencias pequeñas en los valores Richter (7,2 a 3,0, por ejemplo) se traducen en diferencias enormes en la intensidad de los terremotos.
Si te pica la curiosidad y quieres saber un poco más, visita el siguiente enlace.