1.1 Las propiedades de la exponencial
Vamos a comenzar viendo lo que tiene que cumplir la base para que de verdad tengamos una función exponencial.
 |
| 3. Imagen simoncpage bajo licencia Creative Commons |
Tú mismo lo vas a descubrir en la siguiente escena.
En esta escena tenemos representada la función f(x) = ax, y a "a" podemos darle distintos valores arrastrando el deslizador. Muévelo y observa lo que pasa con la representación gráfica.
Para afinar un poco más la precisión, puedes pinchar sobre el punto marrón con el botón izquierdo del ratón y mover los cursores de izquierda y derecha.
Contesta a las siguientes cuestiones manipulando la escena anterior:
1. ¿Para qué valores de "a", la función es creciente?
2. ¿Para qué valores la función es decreciente?
3. ¿Qué ocurre si a = 1? ¿Y si es igual a 0?
4. ¿Qué pasa si "a" es negativo?
5. ¿Qué valor debe, por tanto, tener la base para que haya función exponencial?
Una función exponencial es una función de la forma
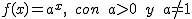
La gráfica de la función siempre es de la forma:
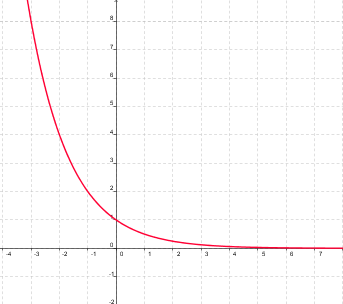 |
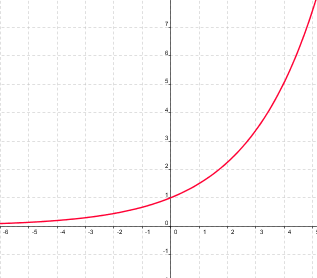 |
| f(x) = ax, 0<a<1 |
f(x) = ax, a>1 |
 |
En la escena, puedes observar también que si la base es mayor que 1, mientras más grande sea más empinada está la curva, es decir, crece más deprisa.
Por contra, si la base está entre 0 y 1, mientras más pequeña sea, o sea, mientras más cerca de cero esté, más empinada es la curva, y por tanto, más rápidamente decrece.
Luego si el valor de la base está próxima a 1, la curva se suaviza, llegando a ser una recta (función constante) si a=1, pues 1 elevado a cualquier cosa es 1. Por contra, si nos alejamos de 1, la subida o bajada de la curva se hace más brusca.
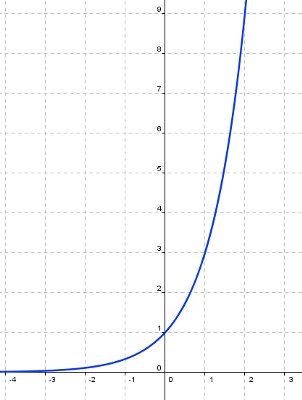
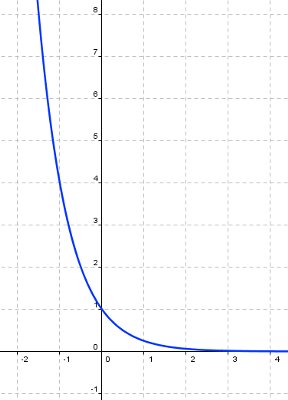
Asocia cada gráfica con su función:
1.- 
|
f(x)=1,5x
| |
|
f(x)=-3x
| |
|
f(x)=3x
| |
|
f(x)=0,25x
|
|
f(x)=1,5x
| |
|
f(x)=-3x
| |
|
f(x) = 2,5x
| |
|
f(x)=0,25x
|
Otras propiedades de la función exponencial:
- El dominio es todos los números reales,
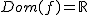
- El recorrido, todos los números positivos;
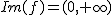
- No corta al eje OX y siempre corta al eje OY en el punto (0,1), pues, cualquier número elevado a 0 es 1.
- La recta y=0 es una asíntota horizontal.
Para relajarnos un poquito, en este vídeo tienes unos cuantos ejemplos de nuestro entorno en los que apacecen una función exponencial.