1.2 Cambiamos de vestido.

 Dibujo sobre una pared en la que una figura desplaza a otra hacia la izquierda
 4. Imagen de seretuaccidente bajo licencia Creative Commons.

Lo habitual, es que en una situación en la que aparece una exponencial, esta no sea exactamente un número elevado a x, sino que haya alguna pequeña variación como cantidades sumando o multiplicando a la función o al exponente.

Vamos a ver qué efecto produce en la gráfica de una función exponencial estas transformaciones.

En la siguiente escena, aparece representada la función f(x) = 2x, aunque puedes cambiar la base en el control que aparece en la línea inferior.

Con el control "k", puedes sumarle a la "x" unidades en el exponente, es decir, representar la función f(x+k), y con el control "h" puedes sumar valores al resultado final de la función, o sea, hacer f(x) + h.

Manipula los controles y observa lo que pasa.

 

Applet modificado del original de Joan Carles Fiol Colomar en Descartes bajo licencia Creative Commons

 

Esta unidad interactiva requiere la máquina virtual de Java J2RE.
Icono IDevice Importante

Si sumamos o restamos una cantidad en el exponente, es decir, en la variable x, desplazamos la gráfica hacia la izquierda o derecha respectivamente.

Si sumamos o restamos una cantidad a la función, desplazamos la gráfica hacia arriba o hacia abajo respectivamente.


Vamos a ver ahora lo que ocurre cuando en lugar de sumar multiplicamos en el exponente o en la función:

En la primera escena multiplicamos la función por "k", mientras que en la segunda multiplicamos la x del exponente por "h". En la tabla que acompaña cada escena puedes ver los cálculos que se están haciendo.

Modifica los controles y observa los cambios de la función. Puedes variar el zoom para ver mejor la función.

Applets descartes de Pilar Flores Fernández en Descartes bajo licencia Creative Commons.

Esta unidad interactiva requiere la máquina virtual de Java J2RE. Esta unidad interactiva requiere la máquina virtual de Java J2RE.

AV - Pregunta Verdadero-Falso
Contesta a las siguientes cuestiones a partir de lo que veas en las dos escenas anteriores.


1.- Si la base es mayor que 1 y multiplicamos la función por un número positivo mayor que 1, la función crece más rápidamente.

Verdadero Falso


2.- Si la base es mayor que 1 y multiplicamos la función por un número positivo menor que 1, la función también crece más rápidamente

Verdadero Falso


3.- Si la base es mayor que 1 y multiplicamos la función por un número negativo (k<0), la función sigue siendo creciente.

Verdadero Falso


4.- Si multiplicamos el exponente por un número negativo, la función exponencial cambia de forma, es decir, si la base es mayor que 1 pasa a ser decreciente y si es menor que 1 pasa a ser creciente.

Verdadero Falso


5.- Si se multiplica en el exponente, la función nunca puede ser negativa.

Verdadero Falso


6.- La función f(x)=32x crece mucho más rápido en los números positivos que la función y= 3x.

Verdadero Falso
Icono IDevice Para saber más

En este primer punto del tema hemos visto las funciones exponenciales más elementales, pero éstas pueden complicarse mucho más. Existen numerosos fenómenos que obedecen a modelos exponenciales pero en los que la expresión que aparece en el exponente no es sólo "x", sino que puede haber un polinomio, o una función racional o cualquier tipo de función.

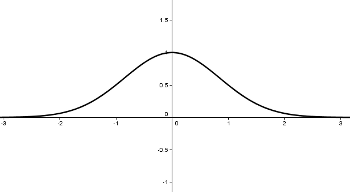
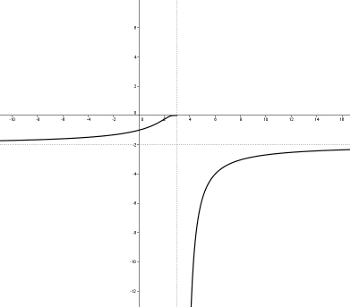
Por ejemplo, las siguientes gráficas corresponden a funciones exponenciales y sin embargo sus gráficas no tienen nada que ver con las que acabamos de estudiar en el tema.

Eso sí, en ellas puedes comprobar que siempre el dominio de la exponencial coincide con el dominio de la función que hay en el exponente.



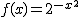
« Anterior | Siguiente »