2.3 La unión hace la fuerza.
 |
Después del apartado anterior suponemos que ya eres capaz de calcular probabilidades de sucesos fáciles, por lo tanto, vamos a ver si complicamos un poco la cosa. Ya viste en el apartado 1.3 que los sucesos se podían operar y es verdad que a veces lo que queremos que suceda es una operación entre dos o más sucesos. Por ejemplo, si queremos saber la probabilidad de que el autobús que estamos esperando en la parada sin marquesina tarde más de 15 minutos o que se levante la niebla que hace y que está entorpeciendo la circulación, está claro que está formado de la unión de dos sucesos, que el autobús tarde y de que además se despeje el día.
En este apartado vamos a ver como trabajar con la probabilidad de la unión y de la intersección. Aunque no creas que es algo más complicado que lo que hemos hecho. Supongo que recordarás el último ejercicio que has hecho, el de sacar cartas de una baraja. Uno de los sucesos era sacar una carta que fuese de copas o de bastos. Eso corresponde a la unión de dos sucesos, sacar copas y sacar bastos. También el suceso de sacar oros o una figura era la unión de dos, sacar una carta de oros y sacar una figura. La diferencia entre los dos es que en el primer caso los dos sucesos son incompatibles, es decir, no podemos sacar a la vez una carta de copas que sea de bastos, mientras en el segundo caso son compatibles. Por último, el suceso de sacar una copa que no sea figura es la intersección de dos sucesos, sacar copa y sacar una carta que no sea figura.
Se define la probabilidad de la unión, en sucesos compatibles, como la siguiente suma:
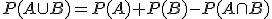
Si los sucesos son incompatibles, como su intersección es el suceso imposible cuya probabilidad es cero, la fórmula anterior se reduce a la expresión:
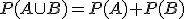
Extraemos una carta de una baraja, halla la probabilidad de obtener una carta:
- De copas o bastos.
- De oros o figura.
1. Si conocemos que 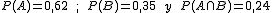 , la probabilidad de la unión sería igual a
, la probabilidad de la unión sería igual a 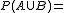 .
.
2. Si ahora conocemos los datos 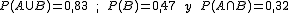 ; la probabilidad del suceso A sería P(A)=
.
; la probabilidad del suceso A sería P(A)=
.
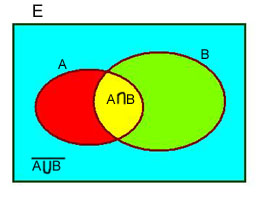 |
A veces, en lugar de conocer directamente las probabilidades de los sucesos A o B, conocemos los de sus contrarios, por ello es interesante recordar que A y B son dos sucesos que forman parte de un espacio muestral más general. Para tenerlo presente vamos a fijarnos en el siguiente dibujo.
El cuadro representa el espacio muestral en el que hay dos sucesos compatibles. El suceso A estaría formado por los colores rojo y amarillo, el B por el amarillo y verde. Los colores rojo, amarillo y verde corresponderían a la unión de A y B. El amarillo a la intersección de los dos sucesos y el color azul corresponde al contrario de la unión de los dos sucesos.
Como aplicación, el suceso contrario a A estaría formado por la parte azul y verde y el contrario al B por la parte roja y azul. Veamos la aplicación de esto en un ejemplo.
¿Qué porcentaje lee ambos periódicos?
Ten presente que si un suceso tiene un porcentaje del 25% equivale a decir que su probabilidad es 0,25.
Para acabar esta parte, realiza una serie de ejercicios en el applet de EDAD, que incluimos a continuación, y a la que llegas también a partir del siguiente enlace. Mira primero los ejemplos que aparecen resueltos y pulsa después en el botón para hacer los ejercicios.
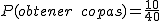 y la de
y la de 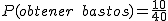 .
.
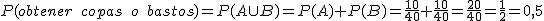
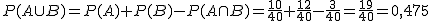
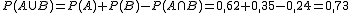
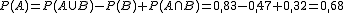
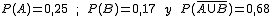
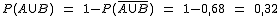
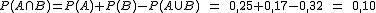
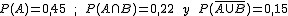 .
.
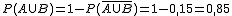 .
.
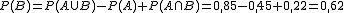 .
.