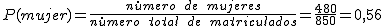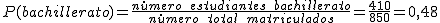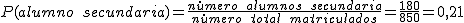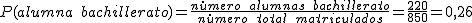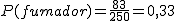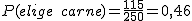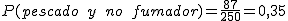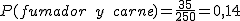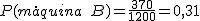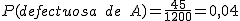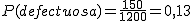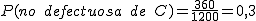3. ¡Cómo ayuda una buena tabla!
 |
Como suele decirse, a estas alturas de la película ya sabrás quién es el asesino. Hablando en serio, seguro que ya sabes calcular las probabilidades de muchos sucesos aleatorios, es decir, ya podrías decidir entre distintas opciones que te propusieran calculando las probabilidades de que ocurran los distintos sucesos. Está claro que si tienes una bolsa con una serie de bolas que sabes cuáles son, es fácil calcular cuál es la probabilidad teórica de que salga una bola de cualquier
 |
color, pero el problema es que en la vida corriente no es fácil conocer cuál es la probabilidad de que ocurra un suceso, por ejemplo, la probabilidad de que elegido un recién nacido en un gran hospital, sea niña o niño.
Muchas veces la probabilidad de que ocurra un suceso se hace coincidir con su frecuencia relativa. Por ejemplo, en el apartado anterior hemos hablado del porcentaje de personas que leían El País en una determinada ciudad, lo lógico es suponer que si elegimos una persona al azar, la probabilidad de que esa persona lea el periódico coincide con su proporción, como hemos hecho en el caso anterior. Por eso, cuando no sabemos exactamente la probabilidad de un suceso, la sustituimos por la frecuencia relativa de cualquier estudio que conozcamos.
En la siguiente escena podrás realizar unas actividades en las que aproximas la probabilidad por la frecuencia relativa. Estas actividades han sido extraídas del proyecto ed@d
A veces esos estudios estadísticos vienen referidos a dos variables distintas y están distribuidos en una tabla.
Importante
En las Ciencias Sociales es muy corriente presentar datos de un estudio estadístico referidos a dos variables mediante una tabla de doble entrada llamada tabla de contingencia en la que se distribuyen los valores de cada variable mediante filas y columnas. Suele ser muy utilizadas cuando se trabajan con poblaciones en estudios sanitarios, económicos, industriales, etc.
A partir de esa tabla es muy fácil calcular la probabilidad de que ocurra cualquier suceso.
 |
Vamos a ponerte un ejemplo de nuestra relación cotidiana. Podemos estudiar el número de personas que están matriculadas en el curso 2009/2010 en la Secundaria y el Bachillerato a distancia, separándolas por hombres y mujeres y, tras redondear los datos, obtenemos la siguiente tabla.
 |
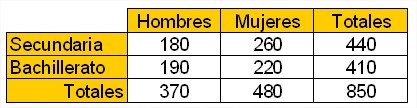A partir de esa tabla es muy fácil calcular probabilidades, veámoslo en el siguiente ejercicio.
Ejemplo o ejercicio resuelto
Si elegimos un alumno al azar entre los matriculados en la secundaria y bachillerato a distancia cuál sería la probabilidad de que fuera:
- Mujer.
- Estudiante de Bachillerato.
- Un alumno de Secundaria.
- Una alumna de Bachillerato.
AV - Actividad de Espacios en Blanco
 |
¿Recuerdas a Mercedes, la estadística que conociste en la Unidad 5? Pues Mercedes ha estado haciendo un estudio para ver si en los clientes de restaurante influye el hecho de ser fumador o no a la hora de elegir carne o pescado. Ha realizado una tabla del estudio, pero cuando le hemos echado un vistazo, aún no la había terminado de rellenar. Lo primero que debes hacer es rellenar la tabla siguiente:
| Fumador |
No fumador |
Total |
|
| Carne |
35 |
|
|
| Pescado |
87 | 135 |
|
| Total |
|
250 |
Si elegimos una persona al azar de las que se han entrevistado, responde las siguientes cuestiones redondeando a dos cifras decimales:
- La probabilidad de que sea fumador es .
- Hay una probabilidad de de que sea aficionado a la carne.
- Puede ser aficionado al pescado y no fumador con una probabilidad de .
- La probabilidad de que le guste la carne y fumar es de .
AV - Reflexión
 |
En una determinada fábrica tienen tres máquinas A, B y C dedicadas a la fabricación de memorias externas USB. Periódicamente se realiza un estudio para ver el número de elementos defectuosos que fabrica cada una de las máquinas. Sabemos que del total de 1050 pendrive no defectuosos, 375 provienen de la máquina A, que ha fabricado en total 420 de las piezas estudiadas y 360 no defectuosos provienen de los 410 fabricados por la máquina C. Además la máquina B ha fabricado 55 piezas defectuosas de las estudiadas. Escribe una tabla de contingencia donde se relacionen las tres máquinas con el hecho de que las piezas sean o no defectuosas. Si elegimos una pieza al azar, entre las estudiadas, ¿cuál es la probabilidad de que?
- La haya fabricado la máquina B.
- Sea una de las defectuosas fabricada por la máquina A.
- Sea una pieza defectuosa.
- La haya fabricado la máquina C y no sea defectuosa.
