2.2 Cuando todo puede pasar igual.

Décimo de lotería de Navidad

Siempre que se oyen cuentos sobre gente que hace trampas en el juego se habla de cartas marcadas, monedas o dados trucados, ruletas manipuladas y siempre en la línea de conseguir que los resultados que se esperan que tengan determinada probabilidad se vean alterados. Por ejemplo, todos suponemos que en cualquier moneda, si la lanzamos, tiene las mismas oportunidades de salir cara que cruz. Aunque esa idea nos comienza a cambiar si elegimos otros juegos. Por ejemplo, aunque nuestra mente nos diga lo contrario, todos pensamos que el número 00001 tiene menos posibilidades de salir en la lotería que el número 81782.


Hay por supuesto experimentos en los que los resultados no tienen las mismas posibilidades de salir. Por ejemplo, el día que hará mañana en Málaga es algo que no sabemos, pero no todos los resultados tienen la misma oportunidad de suceder. Si estamos en verano es mucho más probable que haga sol que no que llueva y prácticamente ninguna posibilidad de que nieve. Sin embargo, en este apartado no vamos a estudiar esos experimentos en general sino que vamos a estudiar aquellos en los que todos los resultados tienen la misma oportunidad de suceder.

Icono IDevice Importante
Se llaman sucesos equiprobables aquellos que tienen la misma probabilidad de suceder. Por ejemplo, en una moneda no trucada, los sucesos salir cara y salir cruz tienen las mismas posibilidades de ocurrir. De la misma manera, en una baraja normal de cartas, si extraemos una al azar, cualquiera de las cartas tiene la misma posibilidad de salir.

Icono IDevice Curiosidad
Hay autores que consideran que la baraja de cartas española es la principal aportación de nuestro país a los juegos de azar. No se sabe exactamente si es una invención española o provino de otros países europeos, como Italia, lo cierto es que en la Edad Media era un juego muy extendido. Ya en 1331 el rey Alfonso XI promulgó una ley prohibiendo que sus caballeros jugaran a ese "nefasto juego". 
Carta 1 de cada palo de la baraja española

 

La baraja estándar está formada por 40 cartas divididas en cuatro palos que representaban a la sociedad medieval. Los oros representaban a la nobleza, las copas al clero, las espadas a los militares y guerreros y por último los bastos representaban al pueblo llano, los campesinos y labradores.

 

Cada palo está formado por 10 cartas, las primeras numeradas del 1 al 7 y después tres figuras: la sota (marcada con un 10), el caballo (con el número 11) y el rey (con la puntuación 12). Es posible jugar con una baraja extendida en donde aparezcan cartas para 8 y 9, en cuyo caso la baraja llega a tener 48 cartas.


Sota, caballo y rey de oros
Vamos a poner un ejemplo de como hallar la probabilidad de un suceso en un experimento donde los resultados son equiprobables. Vamos a considerar una baraja de cartas española estándar. La probabilidad de salir cada una de las cartas es la misma, llamémosla p. Si sumamos todas las probabilidades de los sucesos elementales, es decir, las 40 cartas, tendremos que la suma vale 40·p y que eso debe ser igual a 1. Por tanto, si 40·p = 1, cada carta tiene la probabilidad de salir igual a .

 

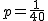Si ahora queremos hallar la probabilidad de que al extraer una carta nos salga una figura de oros, basta sumar las probabilidades de todos los sucesos elementales que forman ese suceso. En nuestro caso:

 

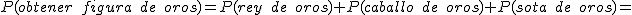
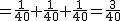
Como podemos ver, en el numerador tenemos la cantidad de cartas que corresponden al suceso pedido, es decir, figura de oros, y en el denominador el número total de cartas. Esto nos lleva a la siguiente regla.

Icono IDevice Importante
En un experimento con resultados equiprobables, la probabilidad de un suceso es el cociente entre el número de resultados favorables al suceso partido por el número de resultados posibles del experimento, es decir, el número de sucesos elementales. Este resultado se conoce como Regla de Laplace.

 

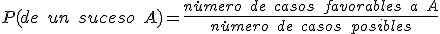
Por ejemplo, si lanzamos un dado cúbico, la probabilidad de obtener un múltiplo de 3 sería 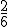ya que hay dos sucesos favorables (el 3 y el 6) frente a seis posibles (los resultados del espacio muestral, 1, 2, 3, 4, 5, 6).


Icono IDevice Para saber más
Imagen de Laplace
2. Imagen de Pierre-Simon Laplace de dominio público tomada de wikimedia commons.

Pierre Simon Laplace, matemático francés que vivió a caballo entre el siglo XVIII y XIX fue quien organizó la teoría matemática de la probabilidad en su obra Théorie analytique des probabilités. También trabajó otras ramas de las matemáticas, como la astronomía. Es famosa la frase que le dio a Napoleón cuando éste le recriminaba por qué en sus escritos de mecánica celeste no apareciera Dios. Laplace le contestó: "Señor, no he necesitado esa hipótesis".

 

En el siguiente vídeo tienes la una parte del programa sobre la revolución francesa y las matemáticas de la serie Universo Matemático de Antonio Pérez Sanz. En esta parte se presentan datos biográficos de la vida de Laplace.

 

 



Icono de iDevice Ejemplo o ejercicio resuelto
Dado de 20 caras

Tenemos un dado con 20 caras numeradas del 1 al 20 (cuya figura geométrica es el polígono regular llamado icosaedro), lo lanzamos y nos fijamos en qué número obtenemos. Queremos saber que probabilidad hay de obtener un número que sea:

  1. Múltiplo de 5.
  2. Mayor que 12.
  3. Mayor que 4 y menor que 12.

 


En el siguiente enlace puedes practicar la aplicación de la Regla de Laplace.

Regla de Laplace

Icono de iDevice AV - Actividad de Espacios en Blanco
Vamos a realizar el experimento de extraer una carta de una baraja española de 40 cartas. Calcula las siguientes probabilidades y recuerda escribir el valor en forma decimal (con ,) y utilizando un máximo de tres cifras decimales para no tener que redondear (no escribas 0 al final del decimal).
  1. La probabilidad de obtener un 5 es .
  2. La probabilidad de obtener una figura es .
  3. Si queremos obtener la sota de espada, la probabilidad es .
  4. Un número menor que 5 tiene una probabilidad de de salir.
  5. Hay una probabilidad de de obtener copas o bastos.
  6. Obtener una carta de oros o una figura tiene una probabilidad de .
  7. La probabilidad de obtener una carta de copas que no sea figura es .
  

Icono IDevice Curiosidad

Seguro que en alguna ocasión has jugado a la lotería e incluso puedes que seas una persona aficionada a otro tipo de sorteos como los de la ONCE. Normalmente, siempre vemos en los medios de comunicación las personas que han ganado un premio, pero no se entrevista a los miles que no han conseguido nada. A veces no nos creemos la dificultad de que en un sorteo pueda tocarnos un premio, sin embargo, en el siguiente vídeo se ejemplifica esa dificultad de una manera muy clara.

 

 

 
 
 
 
 
 

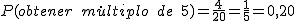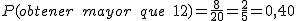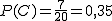« Anterior | Siguiente »