2.1 Es muy probable.
 |
| 1. Foto de Alvarélio bajo licencia Creative Commons. |
Imagina por un momento que sueles entrenar un equipo de futbol juvenil. En el partido de este sábado acaban de pitar un penalti a favor de tu equipo y tienes que decidir quien lo tira y quieres elegir al que tenga más posibilidades de marcarlo. Tienes dos jugadores especialistas en lanzamientos de pena máxima, uno ha lanzado este año 12 penaltis y ha marcado 8, el otro ha lanzado 8 y conseguido 6 goles. ¿A quién elegirías?
En este apartado vamos a ver como asignarle a un suceso aleatorio una cantidad que mida lo probable o improbable que sea el que se realice.
Si estamos pensando en cuál de los dos jugadores elegir, quizás sea buena idea tener en cuenta la proporción de aciertos al lanzar el penalti. En el primer jugador sería 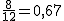 y en el segundo sería
y en el segundo sería 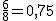 , es decir, elegiríamos al segundo.
, es decir, elegiríamos al segundo.
 |
En el applet que encontrarás en el siguiente enlace, puedes simular el lanzamiento de un número de monedas. Puedes ir lanzando uno a uno, o hacer lanzamientos múltiples de 100 ó 2000 grupos de monedas. Queremos que vayas haciendo lanzamientos, primero uno a uno y después en bloque para que veas que al principio las frecuencias relativas van cambiando bruscamente, pero a medida que aumenta el número de tiradas esos cambios son cada vez más pequeños. Puedes elegir el número de monedas que lanzas e incluso puedes elegir si quieres trucar las monedas, es decir, que la probabilidad de que salga cara y de que salga cruz no sea la misma.
En el siguiente enlace tienes una ruleta que puedes diseñar a tu gusto. Vas haciendo tiradas aleatorias y te compara la frecuencia relativa del suceso con la probabilidad teórica. Si haces muchos lanzamientos puedes comprobar como las primeras se acercan a las segundas.
La probabilidad de un suceso A suele representarse por P(A) y tiene las siguientes propiedades:
- La probabilidad de un suceso es siempre un número comprendido entre 0 y 1. La probabilidad del suceso seguro es 1 y la del suceso imposible es 0, es decir,
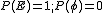 .
. - La suma de las probabilidades de los sucesos elementales vale 1.
- La suma de un suceso y de su suceso contrario vale 1:
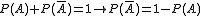
- La probabilidad de un suceso es igual a la suma de las probabilidades de los sucesos elementales que lo forman.
Vamos a ver su aplicación en el siguiente ejercicio.
 |
Jorge es un bromista y a veces lleva un dado trucado para quedarse con sus amigos que intentan jugar con él sin saber que les hace trampas. Las probabilidades que tiene ese dado de sacar las caras del 1 al 5 son las siguientes:
P(1) = 0,15 ; P(2) = 0,20 ; P(3) = 0,10 ; P(4) = 0,15 ; P(5) = 0,20.
- ¿Cuál sería la probabilidad de obtener un 6 con ese dado?
- Si lanzamos el dado, ¿qué probabilidad hay de obtener un número par?
- ¿Y de obtener un múltiplo de 3?
- En ese tipo de dado la probabilidad de obtener un 2 es y la de obtener un 3 es .
- La probabilidad de obtener un número primo es .
Pista para resolverlo: Llama p a la probabilidad de cada número impar [P(1)=P(3)=P(5)=p] y entonces la probabilidad de obtener cada par será 3p [P(2)=P(4)=P(6)=3p]. Suma todas las probabilidades, iguala la suma a 1 y halla p, y con ello cada probabilidad.
Escribe la probabilidad con dos cifras decimales y señala la parte decimal con ",".
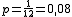 y
y 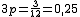 . Luego la P(2) = 0,25 y P(3) = 0,08.
. Luego la P(2) = 0,25 y P(3) = 0,08.