2.2. Sumar, restar, duplicar
 |
| 10510 de Bibliomata, CC by-cn-sa 2.0 |
Esta es mi décima travesía de Cádiz a la Habana, pero la primera como segundo oficial del cargero. Por fin estoy preparado y autorizado para utilizar el sextante e indicar el rumbo de la nave. Cinco años de preparación y duro aprendizaje.
Hallar el ángulo que determinan el Sol o la Osa Mayor con respecto al horizonte, consultar las tablas trigonométricas, realizar los cálculos aplicando las enrevesadas fórmulas, averiguar la latitud o la más complicada longitud, fijar el rumbo, determinar las millas que llevamos navegadas o las que nos faltan para llegar a Cuba. Todo lo anterior corresponde a mis atribuciones de capitán de fragata. Claro, siempre es necesario contar con el visto bueno del Comandante, pero tengo comprobado que confía en mí.
De esta forma razonaba un joven Capitán de fragata de la flota española que realizaba la travesía atlántica de la península a América, a medidados del siglo XIX.
Y toda esa preparación y cálculos fueron necesarios hasta bien entrado el siglo XX. Pero gracias a la aparición de aparatos eléctrónicos, radares, calculadoras, ordenadores, satélites artificales, comunicaciones digitales, GPS ... esos conocimientos han quedado para el recuerdo.
Ya hemos visto que la calculadora científica nos facilita y agiliza el trabajo con las razones trigonométricas de un ángulo. En este apartado veremos algunas de las fórmulas que nuestro joven marino seguro que utilizó para conocer el seno o la tangente de esos ángulos de inclinación que el Sol o las estrellas, determinaban con el horizonte.
Actividad
Razones trigonométricas de la suma de dos ángulos α y β
AV - Reflexión
 |
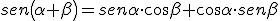
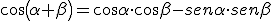
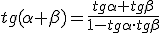
| Big Dipper de Otto Phokus, CC by-sa 2.0 |
Nuestro joven oficial le toca guardia en la estrellada noche altántica. Coge el sextante y para saber a qué latitud navegan, mide el ángulo de elevación de la Estrella Polar. Sus cálculos le indican que están a 55º grados norte.
Para saber los grados que se han desviado de su ruta, necesita conocer el seno de esa latitud. Mira en las tablas y comprueba que en ellas sólo aparecen los senos hasta 45º.
¿Podríamos ayudarles aplicando alguna de las fórmulas anteriores? Por ejemplo, si escribimos 55º como 30º+25º.
Halla el sen 55º aplicando la primera fórmula anterior. Utiliza la calculadora para las razones trigonométricas de 30º y 25º. Para terminar, halla el sen 55º con la calculadora, y comprueba si coinciden los resultados.
Actividad
Veamos ahora las fórmulas análogas a las anteriores para la diferencia de dos ángulos.
AV - Actividad de Espacios en Blanco
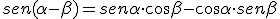
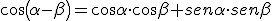
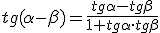
Vamos a comprobar que sen 45º = cos 45º, utilizando la primera fórmula anterior.
Completa los espacios blancos.
Actividad
Por último, las razones trigonométricas del ángulo doble.
AV - Reflexión
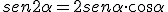
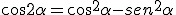
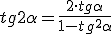
El seno de 180º vale 2, está claro. sen 180º = sen (2·90º) = 2·sen90º = 2·1 = 2.
Pero si lo hago con la calculadora me sale que es cero. ¿En qué me he equivocado?
Pre-conocimiento
Por cierto, ¿te has dado cuenta de que tanto el seno como el coseno de un ángulo nunca es más pequeño que -1, ni mayor que 1? Dicho de otra manera, varían en el intervalo [ -1, 1].
¿A qué es debido?
En el caso de los ángulos agudos, por la propia definición. Recuerda, el seno era el cateto opuesto dividido por la hipotenusa, y el coseno el cateto contiguo entre la hipotenusa. Y la hipotenusa siempre es el mayor de los lados en un triángulo rectángulo.
Para el resto de los ángulos, haz memoria, definíamos el seno y el coseno en una circunferencia goniométrica, de radio 1. Por tanto, los valores que podían tomar variaban entre -1 y 1.