3. La hipotenusa está debajo
Para terminar el tema dedicado a la trigonometría, vamos a presentar dos situaciones en las que debemos encontrar elementos desconocidos de un triángulo rectángulo, haciendo uso de la trigonometría. Esto nos ayudará a resolver las dudas que se nos plantean.
En la primera se nos enfrentamos al reto del determinar la latitud de una población, con tan solo mirar al Sol.
Si a lo largo de todo un año, tuviéramos la paciencia de fijarmos en la posición que ocupa el Sol en el cielo, a la misma hora del día y en un mismo punto de nuestra ciudad, nos llevaríamos alguna sorpresa. De ningún modo esa posición es fija. Al contrario, va describiendo una curva con la silueta de un ocho inclinado, como podemos apreciar en el siguiente vídeo.
Es lo que ha hecho el autor del vídeo, fotografiar el Sol durante un año, a la misma hora, y en el mismo sitio. La curva que describe se llama analema. El punto más alto del analema corresponde al día de entrada del verano. El punto más bajo al del invierno. Por último, los puntos donde se cruza el ocho corresponden a los días de entrada del otoño y la primavera.
En la actualidad, los habitantes de las ciudades occidentales no tenemos tiempo para mirar al cielo. Sobre todo de noche, nos es imposible disfrutar del conmovedor espectáculo de miles de estrella parpadeando, debido a la contaminación lumínica y la vida acelerada.
Pero hasta hace algo más de un siglo, la observación del Sol, la Luna y otros cuerpos celestes permitió a los seres humanos situarse en la Tierra, viajar y medir distancias.
Ahora, para conocer el dato de la latitud de una ciudad, nos basta con buscar en internet. Pero también es posible saberlo si nos detenemos un poco y dedicamos un rato a mirar al Sol.
Sólo necesitamos conocer el ángulo δ, declinación solar del día de la observación. Además, es imprescindible saber la altura máxima que alcanza el Sol sobre el horizonte ese día. Esa altura máxima se consigue al mediodía, hora solar, y viene determinada por el ángulo α que definen los rayos del Sol con el horizonte. Conocidos estos datos, sabemos que la latitud del lugar Φ, cumple la igualdad Φ = 90º + δ - α.
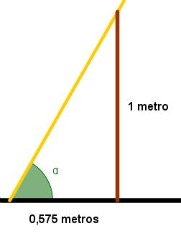 |
En la ciudad andaluza de Osuna, el 9 de abril de 2010 el ángulo declinación solar δ era 7,3166º. Halla la latitud de dicha ciudad, si a las doce del mediodía hora solar, se ha efectuado la siguiente observación para conocer α.
Se ha colocado un palo de longitud 1 metro, verticalmente y se ha medido la sombra que proyectaba sobre el suelo, 0,575 metros.
También es posible hallar la latitud en que nos encontramos mirando al cielo estrellado de la noche. Basta con situar la Estrella Polar y determinar el ángulo de inclinación que tiene respecto del plano del horizonte. En este enlace puedes encontrar más información al respecto.
| |
Ya hemos hablado del seked, la medida que utilizaban los constructores de las pirámides para mantener la inclinación de las pirámides. Un seked es la razón que existe entre el avance y la altura de cada una de las caras de la pirámide. Expresado de otra forma, la razón entre la la anchura y la altura de la pirámide, es decir el cociente 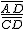 .
.
Es relevante mencionar que todas aquellas pirámides con el mismo seked se encontraban geográficamente cercanas.
 .
.
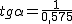 . Utilizando la calculadora científica obtenemos que α=60,10º. Por tanto Φ = 90º + 7,3166º - 60,10º = 37,21º. Que, aproximadamente, es la latitud de Osuna.
. Utilizando la calculadora científica obtenemos que α=60,10º. Por tanto Φ = 90º + 7,3166º - 60,10º = 37,21º. Que, aproximadamente, es la latitud de Osuna.
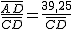 , por tanto
, por tanto 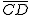 =
= 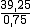 = 52,33.
= 52,33.
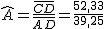 = 1,3333. Lo que quiere decir que
= 1,3333. Lo que quiere decir que 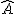 =53,12º
=53,12º
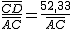 , lo que implica que
, lo que implica que 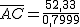 = 65,42 metros.
= 65,42 metros.