1.1. Este viaje ya lo he hecho
| Ya conocemos el resultado que tenemos
al sumarle a un punto cualquiera un vector... el resultado es otro
punto. En la animación de la derecha puedes observar que al sumarle al punto P el vector que aparece en la escena, obtenemos un nuevo punto Q. Practica en la escena para observar cómo se obtienen nuevos puntos a partir de un punto y un vector. |
Instrucciones:
|
| Ahora te proponemos que observes en la
escena de la derecha el efecto que se produce. Fija un punto P arrastrando el punto hasta el lugar que desees. Fija un vector v y ahora observa el punto Q, obtenido como Q=P+t*v, donde t es un número real. Cambia ahora el valor de t arrastrando el punto celeste por el eje de las X. Observa que los distintos puntos Q que se obtienen están alineados, están sobre la misma recta. Puedes hacer que t sea un valor positivo o negativo. Así, todos los puntos que obtienes describen una recta. |
Instrucciones:
|
De esta forma, observando la escena anterior ya conocemos la forma de obtener la ecuación de una recta. Si tenemos un punto 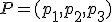 y un vector
y un vector 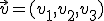 la ecuación de la recta que pasa por el punto
la ecuación de la recta que pasa por el punto  y que sigue la dirección del vector
y que sigue la dirección del vector 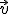 tiene la forma
tiene la forma
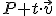
donde 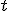 es un parámetro que recorre todos los números reales
es un parámetro que recorre todos los números reales  . así, como los números reales son infinitos, el número de puntos que tiene la recta es infinito, tantos como números reales.
. así, como los números reales son infinitos, el número de puntos que tiene la recta es infinito, tantos como números reales.
Si llamamos a la recta  , la ecuación de la recta se denota:
, la ecuación de la recta se denota:
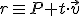
o lo que es lo mismo
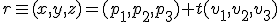
A esta ecuación se le llama ecuación vectorial de la recta. Al vector 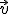 se le denomina vector director de la recta
se le denomina vector director de la recta  .
.
Si queremos ser muy estrictos, desde el punto de vista matemático, la ecuación vectorial de la recta se hallaría sumando al vector que une el origen de coordenadas con el punto P, que se llama vector de posición y que se representa 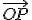 , un múltiplo del vector director.
, un múltiplo del vector director.
Como las coordenadas del vector 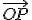 son las mismas que las del punto P, para simplificar los contenidos vamos a trabajar en las ecuaciones de rectas y planos directamente con las coordenadas del punto P.
son las mismas que las del punto P, para simplificar los contenidos vamos a trabajar en las ecuaciones de rectas y planos directamente con las coordenadas del punto P.
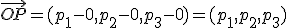
a) Recta  que pasa por el punto
que pasa por el punto 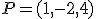 y tiene por vector director
y tiene por vector director 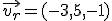 :
: 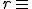 .
.
b) Recta s que pasa por el punto 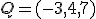 y tiene por vector director
y tiene por vector director 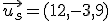 :
: 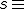 .
.
 |
| Luna. Imagen obtenida del Instituto de Tecnologías de la Educación. |
En el centro de observaciones en el que trabaja Darío quieren realizar un cálculo sobre un meteorito que va a pasar entre La Tierra y la Luna.
Para realizar este cálculo, necesitan conocer la ecuación vectorial de la recta que pasa por la Tierra y la Luna. Para poder calcular esta ecuación saben que las coordenadas de la Tierra son 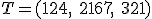 y las coordenadas de la Luna son
y las coordenadas de la Luna son 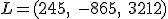 respecto al sistema de referencia que están manejando.
respecto al sistema de referencia que están manejando.
Calcula la ecuación vectorial de la recta que une los dos astros.
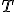 y tiene como vector director el vector
y tiene como vector director el vector 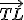 . En este caso la ecuación vectorial de la recta es:
. En este caso la ecuación vectorial de la recta es:
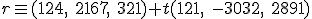
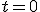 obtenemos el punto
obtenemos el punto 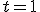 obtenemos el punto
obtenemos el punto 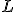 . Compruébalo.
. Compruébalo.
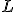 y tiene como vector director el vector
y tiene como vector director el vector 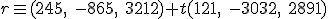
 y para
y para 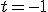 obtenemos el punto
obtenemos el punto 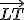 . En este caso la ecuación vectorial de la recta es:
. En este caso la ecuación vectorial de la recta es:
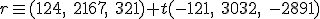
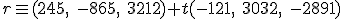
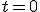 obtenemos el punto
obtenemos el punto