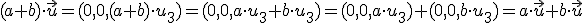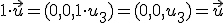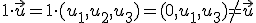1.3 Caminando en el espacio vectorial
|
Como te ha indicado Descartes, ya conoces dos espacios vectoriales sobre los que has estado trabajando, el plano 1.- Si x e y son dos elementos del conjunto V, entonces x+y=y+x. 2.- Si x, z e y son tres elementos del conjunto V, entonces (x+y)+z=x+(y+z). 3.- Existe un elemento del conjunto V que representaremos por 0 de forma que 0+x=x para todos los elemntos x del conjunto V. Lo llamaremos elemento neutro. 4.- Si x es un elemento del conjunto V existe otro elemento que representaremos por -x de forma que x+(-x)=0 para todos los elementos x del conjunto V. 5.- Si k es un número y x e y son elementos del conjunto V, entonces k·(x+y)=k·x+k·y . 6.- Si k y p son números, entonces k·(p·x)=p·(k·x) para todos los elementos x del conjunto V. 7.- Si k y p son números, entonces (k+p)·x=(k·x)+(p·x) para todos los elementos x del conjunto V. 8.- 1·x=x para todos los elementos x del conjunto V.
Así, en el conjunto de todos los vectores del plano,
1.-
2.-
3.-El elemento neutro es
4.- Dado
5.-
6.-
7.-
8.-
Esto mismo sucede en el espacio de tres dimensiones Es una definición demasiado teórica, por lo que vemos a verla con algunos ejemplos: |
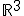 que tienen la forma
que tienen la forma 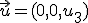 , es decir, que las dos primeras coordenadas son cero, vamos a ver si este conjunto con la operación suma de vectores y la operación del producto de un número por un vector, que ya conocemos es un espacio vectorial.
, es decir, que las dos primeras coordenadas son cero, vamos a ver si este conjunto con la operación suma de vectores y la operación del producto de un número por un vector, que ya conocemos es un espacio vectorial.
Si consideramos el conjunto de todos los vectores del espacio 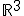 y definimos el producto de un número por un vector como
y definimos el producto de un número por un vector como
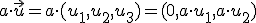
vamos a ver si este conjunto con la operación suma de vectores y la operación del producto de un número por un vector definida, es un espacio vectorial.
El conjunto de los vectores de 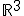 cuya primera y tercera coordenadas son cero, con las operaciones suma de vectores y producto de un escalar por un vector que ya conoces cuya primera y tercera coordenadas son cero, con las operaciones suma de vectores y producto de un escalar por un vector que ya conoces
| |
El conjunto de los vectores de 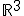 cuya segunda coordenada es cero, con las operaciones suma de vectores y producto de un escalar por un vector que ya conoces cuya segunda coordenada es cero, con las operaciones suma de vectores y producto de un escalar por un vector que ya conoces
| |
El conjunto de los vectores de 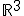 cuya segunda coordenada es el doble que la primera, con las operaciones suma de vectores y producto de un escalar por un vector que ya conoces cuya segunda coordenada es el doble que la primera, con las operaciones suma de vectores y producto de un escalar por un vector que ya conoces
| |
El conjunto de los vectores de 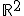 cuya segunda coordenada es 5, con las operaciones suma de vectores y producto de un escalar por un vector que ya conoces cuya segunda coordenada es 5, con las operaciones suma de vectores y producto de un escalar por un vector que ya conoces
| |
El concepto de espacio vectorial se puede aplicar a múltiples conjuntos en matemáticas. Te proponemos que compruebes los dos siguientes puntos:
1.- El conjunto formado por el espacio 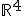 cuyos vectores tienen la forma
cuyos vectores tienen la forma 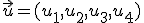 con la operación suma de vectores que conoces y te recordamos abajo, y el producto de un número por un vector que te recordamos, es un espacio vectorial:
con la operación suma de vectores que conoces y te recordamos abajo, y el producto de un número por un vector que te recordamos, es un espacio vectorial:
1.1 Suma de vectores 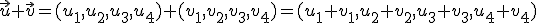
1.2 Producto de un número por un vector 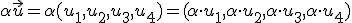
2.- El conjunto formado por las matrices de orden 3x3 con la operación suma de matrices y producto de un número por un matriz es un espacio vectorial
 |
| Pierre de Fermat, imagen tomada de Wikimedia Commons. |
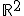 y
y 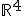 ; el
tratamiento mediante combinaciones lineales se remonta a Laguerre en
1867, quien también definió los sistemas de ecuaciones lineales.
; el
tratamiento mediante combinaciones lineales se remonta a Laguerre en
1867, quien también definió los sistemas de ecuaciones lineales. Un desarrollo importante de los espacios vectoriales se debe a la construcción de los espacios de funciones por Henri Lebesgue. Esto más tarde fue formalizado por Banach en su tesis doctoral de 1920 y por Hilbert. En este momento, el álgebra y el nuevo campo del análisis funcional empezaron a interactuar, en particular con conceptos clave tales como los espacios de funciones p-integrables y los espacios de Hilbert. También en este tiempo, se realizaron los primeros estudios sobre espacios vectoriales de infinitas dimensiones.
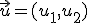 ,
, 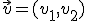 y
y 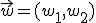 y los números
y los números  y
y 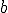 , entonces:
, entonces:
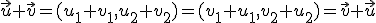 .
.
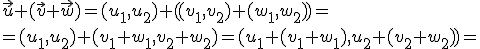
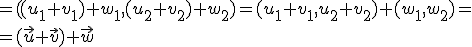
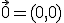 , ya que
, ya que 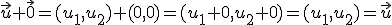
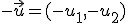 ya que
ya que 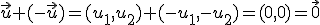
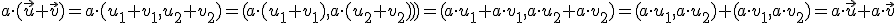 que es un vector de
que es un vector de 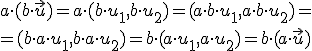
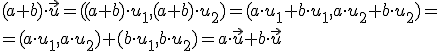
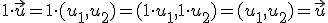
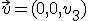 y
y 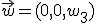 y tomanos dos números
y tomanos dos números 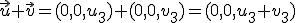 que es un elemento del conjunto ya que las dos primeras coordenadas son cero.
que es un elemento del conjunto ya que las dos primeras coordenadas son cero.
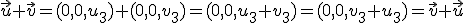
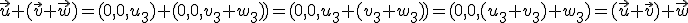
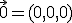 que es un elemento del conjunto ya que las dos primeras coordenadas son cero.
que es un elemento del conjunto ya que las dos primeras coordenadas son cero.
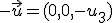 , entonces
, entonces 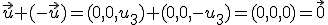
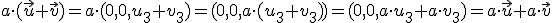 .
.
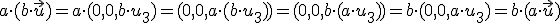 .
.