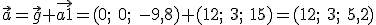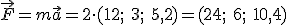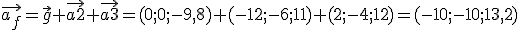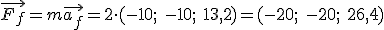1.2 Saltando del plano a otros espacios
|
|
|
Al igual que has trabajado con los vectores en el plano, es decir, en dos dimensiones, de forma análoga puedes trabajar con los vectores en tres dimensiones.
En la imagen de la derecha puedes situar un punto en el espacio a
través de sus tres coordenadas. Así dibujas el punto A. Escribe las coordenadas del punto y gira con el ratón la escena para verlo
|
Ya sabes que, dados dos puntos del plano, las coordenadas del vector
que une el primer punto con el segundo se obtienen restándole a las
coordenadas del segundo punto las coordenadas del primero. En el
espacio ocurre de la misma forma. Dados los puntos del espacio 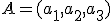 y
y 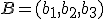 el vector que va del punto A al punto B es:
el vector que va del punto A al punto B es: 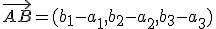
Que no es el mismo que el vector que va del punto B al punto A: 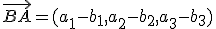
|
REPRESENTANDO VECTORES: Observa en la imagen que te proporcionamos en la que aparece dibujado sobre los ejes cartesianos el vector de coordenadas (1,2,2). Puedes girar la imagen pulsando y arrastrando. Si deseas puedes dibujar varios vectores distintos sin más que arrastrar el punto de finalización del vector a las coordenadas que desees. Dibuja los siguientes vectores que te indicamos: 1.- (3,1,-1) 2.- (1,1,1) 3.- (-2,-2,-2) 4.- (-2,0,0) |
Instrucciones:
|
|
|
| SUMA
DE VECTORES: En la imagen de la derecha podemos observar
como se realiza gráficamente la suma de dos vectores en el espacio
de tres dimensiones. Al igual que en el de dos dimensiones, para
sumar dos vectores de coordenadas (v1,v2,v3) y (w1,w2,w3) el vector
suma es el que resulta de sumar sus coordenadas correspondientes. En
este caso: (v1,v2,v3) + (w1,w2,w3) = (v1+w1,v2+w2,v3+w3) Te proponemos ahora que realices gráficamente las siguientes sumas de vectores y que escribas el resultado de cada apartado en los huecos correspondientes que aparecen más abajo: 1.- (2, -3,5) y (1,0,1) 2.- (-2,4,6) y (3,1,0) 3.- (1,0,0) y (0,1,0) 4.- (2,1,4) y (-2, 1, -2) |
Instrucciones:
|
|
|
3.- ( , , ) 4.- ( , , )
|
RESTA DE VECTORES: En la imagen de la derecha podemos observar como se realiza gráficamente la resta de dos vectores en el espacio de tres dimensiones. Al igual que en el de dos dimensiones, para restar dos vectores de coordenadas (v1,v2,v3) y (w1,w2,w3) el vector resta es el que resulta de restar sus coordenadas correspondientes. En este caso: (v1,v2,v3) - (w1,w2,w3) = (v1-w1,v2-w2,v3-w3) 1.- Al vector (2,3,4) restarle el vector (2,1,0). 2.- Al vector (-2,0,1) restarle el vector (0,2,0). 3.- Al vector (0,0,0) restarle el vector (4,2,1). 4.- Al vector (1,1,1) restarle el vector (2,2,4). |
Instrucciones:
|
|
|
1.- El resultado de la primera resta es ( , , ).
2.- El resultado de la segunda resta es ( , , ).
3.- El resultado de la tercera resta es ( , , ).
4.- El resultado de la cuarta resta es ( , , ).
|
PRODUCTO DE UN ESCALAR POR UN VECTOR: Multiplicar un
número por un vector es lo mismo que sumar el vector tantas veces
como nos indique el número. Por este motivo, si tenemos un número k
y un vector de coordenadas (v1,v2,v3) el resultado de multiplicarlos
es: k(v1,v2,v3) = (kv1,kv2,kv3) En la imagen de la izquierda puedes observar el resultado de multiplicar un número por un vector. Te proponemos que en los siguientes apartados multipliques el número que aparece por el vector que se acompaña. 1.- Multiplicar el nº 2 por el vector (-1,2,0) 2.- Multiplicar 4 por el vector (-1,1,-1) 3.- Multiplicar 3 por el vector (2,-2,3) 4.- Multiplicar -2 por el vector (-1,1,3) |
Instrucciones:
|
1.- El vector que resulta del producto es ( , , )
2.- El vector que resulta del producto es ( , , )
3.- El vector que resulta del producto es ( , , )
4.- El vector que resulta del producto es ( , , )
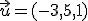 y
y 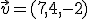 , calcules las coordenadas de los siguientes vectores:
, calcules las coordenadas de los siguientes vectores:
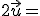 (
,
,
) 2.-
(
,
,
) 2.- 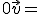 (
,
,
)
(
,
,
)
3.- 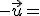 (
,
,
) 4.-
(
,
,
) 4.- 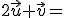 (
,
,
)
(
,
,
)
5.- 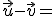 (
,
,
) 6.-
(
,
,
) 6.- 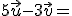 (
,
,
)
(
,
,
)
|
|
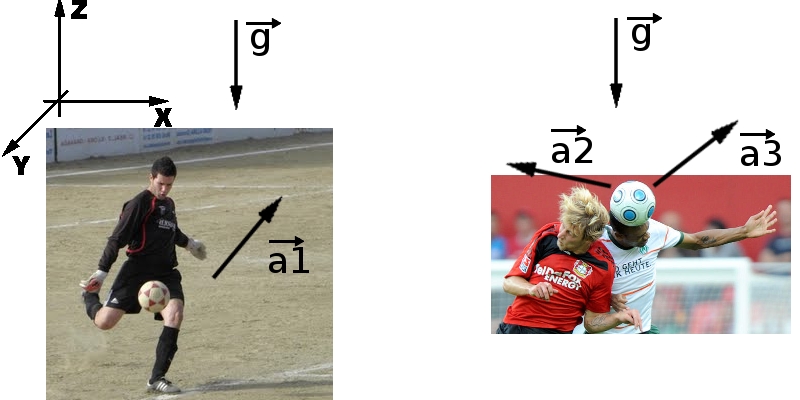
¿Crees que los porteros no marcan goles?, pues observa el siguiente
vídeo. De todas formas, muchas son las cosas que hay que tener en
cuenta a la hora de marcar goles desde tu propia portería. Nosotros
nos vamos a centrar solamente en el saque del portero y en el remate
que pueden hacer dos jugadores. En la imagen inferior observamos un
portero que saca desde su portería en uno de los lances del partido. El
portero, en su saque impacta el balón con una aceleración 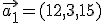 y cuando llega el balón a los jugadores, los dos rematan a la vez de
cabeza cuando el balón llegaba parado. Uno lo hace con una aceleración
y cuando llega el balón a los jugadores, los dos rematan a la vez de
cabeza cuando el balón llegaba parado. Uno lo hace con una aceleración 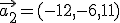 y el otro con una aceleración
y el otro con una aceleración 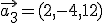 . Si la masa del balón es 2:
. Si la masa del balón es 2:
|
1.- Calcula la fuerza con la que el balón salió impulsado desde la portería.
2.- Calcula la fuerza con la que el balón salió impulsado tras el cabeceo de los dos jugadores.
Debes tener en cuenta que la aceleración de la gravedad es un vector vertical de coordenadas 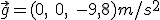 . Ojo,
. Ojo, 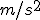 son las unidades de aceleración (metros entre segundos al cuadrado). La
tercera coordenada es negativa debido a que la aceleración de la
gravedad es hacia abajo, hacia la parte negativa del eje Z.
son las unidades de aceleración (metros entre segundos al cuadrado). La
tercera coordenada es negativa debido a que la aceleración de la
gravedad es hacia abajo, hacia la parte negativa del eje Z.
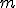 de un cuerpo y la aceleración con la que lo impulsamos
de un cuerpo y la aceleración con la que lo impulsamos 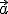 , la fuerza se calcula como el producto de la masa por la aceleración.
, la fuerza se calcula como el producto de la masa por la aceleración.