2.3. No siempre se puede multiplicar
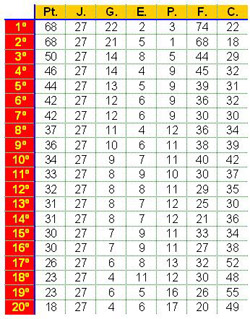 |
Retomamos una tabla que ya pudiste ver al comenzar el tema, la tabla de clasificación de los equipos en un determinado momento de la liga. Hemos quitado el nombre de los equipos, para no crear polémica, pero puedes ver que aparecen los puntos del equipo, los partidos jugados hasta ese momento, entre ellos cuántos se han ganado, empatado o perdido y, por último, los goles a favor y en contra.
Si solamente conociésemos los partidos ganado, perdidos y empatados, podríamos conocer el número de partido jugados. Además, podríamos conocer el número de puntos que tiene el equipo ya que conocemos que obtiene 3 puntos por cada partido ganado, un punto por cada partido empatado y 0 puntos por cada partido perdido.
De la tabla anterior podemos obtener la matriz que contiene el número de partidos ganados, el número de partidos empatados y el número de partidos perdidos de cada equipo:
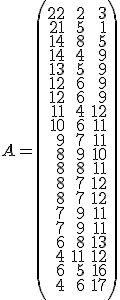
Además, la matriz que nos indica el número de puntos que se le da a un equipo por cada partido ganado, empatado o perdido es la siguiente 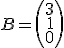
Si a partir de estas dos matrices queremos calcular el número de puntos que tiene cada equipo, deberíamos multiplicar 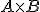 . ¿Sabes cómo hacerlo? .... En la solución te lo explicamos.
. ¿Sabes cómo hacerlo? .... En la solución te lo explicamos.
Si ahora consideramos la matriz 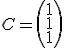 Si multiplicamos
Si multiplicamos 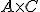 ¿sabes qué obtendríamos?
¿sabes qué obtendríamos?
Y si ahora consideramos la matriz 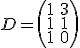 Si multiplicamos
Si multiplicamos 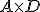 ¿Sabrías hacerlo? ¿sabes qué obtendríamos?
¿Sabrías hacerlo? ¿sabes qué obtendríamos?
No te preocupes, que ahora te desvelamos todos estos secretos
Fijémonos en el producto 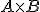 . Lo que hemos hecho es multiplicar cada elemento de la primera fila de la matriz
. Lo que hemos hecho es multiplicar cada elemento de la primera fila de la matriz 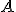 por el elemento correspondiente de la primera columna de la matriz
por el elemento correspondiente de la primera columna de la matriz 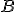 . Para poder hacer lo anterior, el número de elementos que la matriz
. Para poder hacer lo anterior, el número de elementos que la matriz 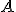 tiene en esa fila (3 elementos en nuestro caso) es el mismo número de elementos que tiene
tiene en esa fila (3 elementos en nuestro caso) es el mismo número de elementos que tiene 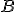 en su columna, en nuestro caso 3 también.
en su columna, en nuestro caso 3 también.
En el ejemplo anterior, la matriz 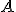 tiene 20 filas y 3 columnas y la matriz
tiene 20 filas y 3 columnas y la matriz 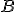 tiene 3 filas y 1 columna. Cuando realizamos el producto
tiene 3 filas y 1 columna. Cuando realizamos el producto 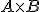 nos resulta una matriz que tiene 20 filas y 1 columna. En resumen.
nos resulta una matriz que tiene 20 filas y 1 columna. En resumen.
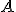 |
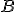 |
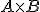 |
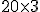 |
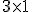 |
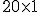 |
Observa qué ocurre en los casos de los productos 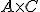 y
y 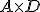 .
.
Piensa si se podría hacer el producto 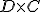 .
.
Si tenemos dos matrices 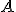 de orden
de orden 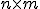 y
y 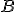 de orden
de orden 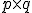 , el producto
, el producto 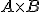 es otra matriz cuyos elementos se obtienen multiplicando de forma ordenada cada fila de la matriz
es otra matriz cuyos elementos se obtienen multiplicando de forma ordenada cada fila de la matriz 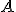 por todas las columnas de la matriz
por todas las columnas de la matriz 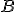 . Así, el elemento que ocupa la posición 3,7 en la matriz resultante es el resultado de multiplicar la fila 3 de la matriz
. Así, el elemento que ocupa la posición 3,7 en la matriz resultante es el resultado de multiplicar la fila 3 de la matriz 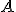 por la columna 7 de la matriz
por la columna 7 de la matriz 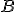 , es decir, cada elemento de la fila 3 de la matriz
, es decir, cada elemento de la fila 3 de la matriz 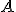 se multiplica por el elemento correspondiente de la columna 7 de la matriz
se multiplica por el elemento correspondiente de la columna 7 de la matriz 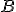 y se suman los resultados.
y se suman los resultados.
Por tanto, el número de elementos que tiene la matriz 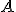 en cada fila (número de columnas de
en cada fila (número de columnas de 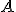 ) tiene que coincidir con el número de elementos que tenga la matriz
) tiene que coincidir con el número de elementos que tenga la matriz 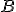 en cada columna (número de filas de
en cada columna (número de filas de 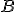 ). en nuestro caso, para que se puedan multiplicar debe cumplirse que
). en nuestro caso, para que se puedan multiplicar debe cumplirse que 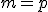 .
.
Dicen que una imagen vale más que mil palabras. Te proponemos el siguiente ejercicio resuelto para que compruebes si has captado como se realiza esta operación con matrices....
Si tenemos dos matrices 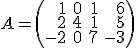 y
y 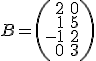
Piensa qué producto podemos hacer 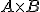 ó
ó 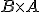 . Cuando lo sepas, calcula el que se pueda hacer o los que se puedan hacer
. Cuando lo sepas, calcula el que se pueda hacer o los que se puedan hacer
Entra en el siguiente enlace y responde a las preguntas del test que aparece para saber lo que has aprendido hasta ahora.
Entra en el siguiente enlace y realiza productos de matrices para comprobar tus destrezas. Cada vez que pulses el botón "Autogenerar" aparecerán dos matrices nuevas. Cuando hayas realizado el producto, pulsa sobre el botón "Comprobar" para comprobar el resultado.
Ahora te proporcionamos una pantalla para que realices productos de matrices de orden 3X3 y después respondas a las cuestiones que te planteamos.
Practica con matrices que inventes. Solamente debes escribir los números en las casillas de las matrices A y B y los resultados aparecerán en la matriz C. Es decir, escribe dos matrices cualesquiera y halla su producto, después puedes comprobar el resultado en la matriz C. Debajo tienes botones que te permiten cambiar las matrices de lugar y calcular A*B ó B*A.
Selecciona ahora la opción o las opciones que consideres correctas después de practicar
Siempre podemos hacer el producto AxA
| |
Si podemos hacer los productos AxB y AxC, entonces se cumple que Ax(B+C)=AxB + AxC
| |
AxB es lo mismo que BxA
| |
Bueno, ahora ya conoces bastante sobre las matrices y conoces cómo deben ser dos matrices para poder multiplicarlas. Ahora te pedimos que reflexiones de forma práctica. Para ello te proporcionamos la siguiente ventana en la que vas a poder realizar el producto de las matrices que consideres necesarios. Para ello te damos las instrucciones sobre su uso:
1.- Escribe el orden de la matriz que deseas introducir. Una vez escrito pulsa sobre el botón crear.
2.- Te aparecerá un espacio para que escribas la matriz. Escribe cada elemento en su casilla correspondiente.
3.- Observa que en la parte superior de la matriz aparece su nombre. Por ejemplo m451
4.- Crea otra matriz de la misma forma que hiciste con la anterior.
5.- En la parte inferior, en la que aparece el cuadro "Multiplicar las matrices" escribe el nombre de cada una de las dos matrices que quieras multiplicar y pulsa el botón Multiplicar.
6.- Aparecerá un nuevo cuadro para la matriz resultado. Pulsa sobre el botón "calcular" y habrás obtenido el producto.
Igual que si multiplicas cualquier número por 1 obtienes el mismo número, hay una matriz que tiene el mismo efecto. La matriz identidad I, que viste en el punto 1.2, cumple que si la multiplicas por cualquier otra matriz, al final nos queda esa segunda matriz.
Compruébalo escribiendo cualquier matriz y multiplicándola por la matriz identidad del orden conveniente para poder hacer el producto. Verás que obtienes la matriz del principio.
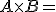

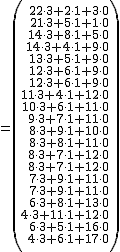
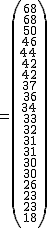 por lo que obtenemos la cantidad de puntos que tiene cada equipo
por lo que obtenemos la cantidad de puntos que tiene cada equipo
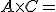


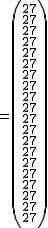 por lo que obtenemos la cantidad de partidos que ha jugado cada equipo
por lo que obtenemos la cantidad de partidos que ha jugado cada equipo
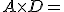
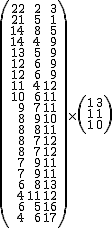
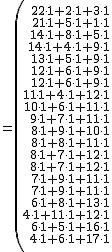

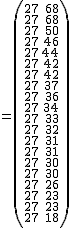 por lo que obtenemos una matriz cuya primera columna recoge el número de partidos jugado por cada equipo y la segunda la cantidad de puntos que tiene cada equipo
por lo que obtenemos una matriz cuya primera columna recoge el número de partidos jugado por cada equipo y la segunda la cantidad de puntos que tiene cada equipo
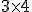 y el orden de la matriz
y el orden de la matriz 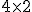 el único producto que podemos hacer es
el único producto que podemos hacer es