1.1. Identidades
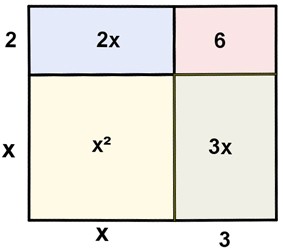 |
En el tema anterior, vimos en el último apartado que:
(x +3)·(x+2) = x2 + 5x +6. ¿Lo recuerdas?
Viendo el área total del rectángulo,
(x+3)·(x+2)
observábamos que ésta era la misma que si se partía en trocitos y se sumaban éstos:
x2 + 2x + 3x +6
Pues bien esta igualdad algebraica es cierta sea cual sea el valor de x. Siempre es verdad.
Vamos a ver otro ejemplo:
En la siguiente escena de Manuel Sada, se muestra el desarrollo del cuadrado de la suma (Dentro del apartado Identidades notables), que si recuerdas era una de las identidades o igualdades notables.
Ve pulsando en los botones para avanzar o retroceder en la escena y en los botones de a y b para cambiar los valores de éstos.
Como puedes ver, siempre se cumple que: (a + b)2 = a2 + b2 + 2ab; sea cual sea el valor que le demos a las letras "a" y "b".
Pues bien esto es lo que se llama una identidad, una igualdad algebraica que siempre es cierta para cualquier valor de las letras. Por eso a esta expresión se le llama también Identidad Notable.
Una Identidad es una igualdad algebraica, esto es una igualdad en la que aparecen números y letras, que siempre se cumple, sean cuales sean los valores de las incógnitas.
Desarrollos similares al que hemos visto con el cuadrado de una suma, existen para las otras dos identidades notables. Puedes verlo en los siguientes enlaces: