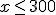4. ¿Y si no es igual?
 |
Has aprendido a calcular valores que cumplen unas determinadas condiciones expresadas mediante ecuaciones. Pero, ¿crees que siempre es posible encontrar uno o dos valores que cumplen esas condiciones? Quizás te sorprenda saber que en la vida cotidiana es corriente que los valores con los que trabajemos no sean únicos, sino que se muevan dentro de un abanico de posibilidades.
Imagina que te encuentras en la necesidad de comprar un coche, lo normal es que tengas fijada una cantidad máxima que te puedas gastar en esa compra, por ejemplo 18.000 euros. Eso no quiere decir que te vayas a gastar exactamente esa cantidad, si no que puedes comprar coches de distintos precios siempre que no exceda de esa cifra. Si, además tienes que pagar el seguro del coche, el impuesto de matriculación, el impuesto de circulación, y demás gastos, todo ello da lugar a una expresión en la que el valor máximo es la cantidad de 18.000 euros.
La expresión que te ha aparecido antes, recibe el nombre de inecuación. No es más que una desigualdad entre dos expresiones algebraicas. Es decir, lo mismo que teníamos en el caso de las ecuaciones, pero cambiando el signo del igual por un desigual.
La forma de trabajar con las inecuaciones es exactamente la misma que en las ecuaciones, salvo un pequeño detalle. En general las operaciones que podemos realizar son las siguientes:
- Podemos sumar o restar cualquier expresión a los dos miembros de la desigualdad sin que cambie la inecuación. Como consecuencia, podemos pasar un sumando de un miembro a otro cambiándole el signo correspondiente.
Ej1: 3x-4 < 4x+1 sumamos 4 en ambos términos: 3x-4+4 < 4x+1+4 operando: 3x < 4x+5
Ej2: 2x+1 > 3x-1 restamos 2x en ambos términos: 2x+1 -2x> 3x-1-2x operando: 1 > x-1 - Podemos multiplicar o dividir por un mismo número positivo los dos miembros de la desigualdad sin que esta cambie. Como aplicación, un número positivo que esté multiplicando en un miembro pasa al otro dividiendo y viceversa.
Ej1: 3x-4 < 4x+1 multiplicamos por 2 ambos términos: 2·(3x-4) < 2·(4x+1) operando: 6x-8 < 8x+2
Ej2: 6x+3 > 12x-9 dividimos por 3 ambos términos: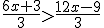 operando: 2x+1 > 4x-3
operando: 2x+1 > 4x-3 - Si multiplicamos o dividimos los dos miembros de una ecuación por un número negativo, la desigualdad cambia de sentido.
Ej1: 8x-4 < 4x+6 dividimos por -2 ambos términos y cambia la desigualdad: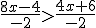 operando: -4x-1 > -2x-32
operando: -4x-1 > -2x-32
Ej2: -6x+3 > -12x-9 dividimos por -3 ambos términos y cambia la desigualdad: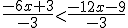 operando: 2x-1 < 4x+3
operando: 2x-1 < 4x+3
Esta última propiedad es fundamental pues es la que suele dar paso a las equivocaciones.
Por ejemplo si tenemos una inecuación que nos dice que -x < -5, y queremos cambiarla de signo, debemos tener en cuenta que también se cambia la desigualdad. Es decir, los valores de x que cumplen la desigualdad anterior son aquellos que verifican que x > 5.
Ahora puedes practicar las propiedades anteriores con la siguiente escena de Descartes. Ten cuidado al dividir entre -2 y -3 de no olvidarte de cambiar la desigualdad. Si colocas todos los círculos en su lugar adecuado, te aparecerá el mensaje Muy Bien.
Escena de Xosé Eixo bajo licencia Creative Commons
Las soluciones de una inecuación no son valores individuales, sino que son todos los valores de un intervalo que verifiquen una determinada condición. Es decir, son los números que son mayores o menores que un determinado valor.
Por tanto, las soluciones de una ecuación serán de la forma x < 4 ó x > 5.
En el ejercicio resuelto encontraste que la expresión del número de pegatinas que se podía comprar sin gastarse más de 80 euros era 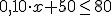 .
.
Despeja el valor de x para saber cuantas pegatinas se pueden comprar.
Resuelve las inecuaciones que tienes a continuación. En la casilla desplegable que hay junto a cada una de ellas deberás escribir el número del 1 al 8 que corresponde a la solución de esa inecuación.
Escena de Xosé Eixo bajo licencia Creative Commons
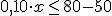 y nos queda
y nos queda  .
.
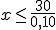 y haciendo la división nos queda
y haciendo la división nos queda