2. Las ecuaciones más simples
Vamos a comenzar ya en este punto la resolución de ecuaciones.En el apartado anterior has visto la diferencia entre ecuación e identidad y cuando un valor es solución o no de una ecuación.
Pues bien, ha llegado el momento de buscar cuál es el valor que sea solución. Para ello vamos a comenzar con las ecuaciones más fáciles, que son las de primer grado.
Applet de Java
 |
| Imagen de eliceo.com bajo licencia Creative Commons. |
Imagínate la siguiente situación: Juan para su nueva tienda quiere contratar a un nuevo empleado, pero para asegurarse de que contrata al mejor, a cada uno de los que acude a la entrevista les hace pasar una pequeña prueba tipo test que consta de 40 preguntas relacionadas con las actividades cotidianas de una tienda de ropa.Pero para asegurarse de que los interesados no responden al azar, decide otorgar un punto a la respuesta correcta y penalizar con 0,4 cada respuesta incorrecta. El criterio que se marca Juan para que pase la prueba es que por lo menos tenga 24 puntos.
A los aspirantes sólo se les informa de que tienen que tener al menos 24 puntos para pasar. Evaristo fue uno de ellos, pero se llevó una gran sorpresa al verse fuera del proceso de selección. Acudió a preguntar y Juan se limitó a contestarle que tenía sólo 21,8 puntos por lo que quedaba descartado.
Evaristo, seguro de sus respuestas, no estaba de acuerdo con esa puntuación pues estaba seguro de que por lo menos había contestado 24 bien, pero no contaba con que las respuestas erróneas descontaban. ¿Tendría razón Juan y no habría aprobado?
Informado ya de que cada respuesta errónea descontaba 0,4 puntos, Evaristo se preguntó, ¿cuántas habré contestado bien?
Actividad
Por ejemplo 3x + 2 = 6.
Recuerda que para despejar x:
- Lo que está sumando pasa al otro miembro restando, y viceversa. Ej: 4x-5 = 8 pasa a 4x = 8 + 5
- Lo que está multiplicando pasa al otro miembro dividiendo, y viceversa. Ej: 4x = 8 Pasa a x=8/4
En la escena puedes ver los pasos a seguir para resolver estas ecuaciones. Pulsa el botón "pasos" para ir avanzando en la resolución.
Si lo deseas, puedes modificar los valores de "a", "b" y "c" en la ecuación.
Escena de Blanca Barroso González bajo licencia Creative Commons
Actividad
Ecuaciones con paréntesis:
- Se eliminan los paréntesis aplicando la propiedad distributiva. Ej: 2·(x-1)=0 pasa a 2x - 2 = 0
- Se pasan a un miembro los términos con x y a otro los números sin x. Ej: 7x + 1 = 2x +16 pasa a 7x -2x = 16 -1 , es decir, 5x = 15
- Se simplifican ambos términos y se despeja la incógnita x. Ej: 5x = 15 puede simplificarse dividendo entre 5: x = 3
Ecuaciones con denominadores:
- Se eliminan los denominadores reduciendo todos los términos a común denominador. También puede conseguirse multiplicando todos los términos por el mínimo común múltiplo de los denominadores y simplificando.
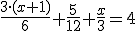como mcm(6,12,3)=12, pasa a 
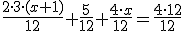y a 6·(x+1) + 5+ 4x = 48- Se eliminan los paréntesis.
- Se continúa igual que antes.
En las dos siguientes escena puedes ver los pasos a seguir para resolver ecuaciones con paréntesis y ecuaciones con denominadores. En ambos casos pulsa el botón "pasos" para ir avanzando en la resolución.
Si lo deseas, puedes modificar los valores de "a", "b" , "c", "e", "f" y "g" de los coeficientes en la ecuación.
Escenas de Blanca Barroso González bajo licencia Creative Commons.
AV - Reflexión
En la siguiente escena puedes resolver distintas ecuaciones aplicando todo lo anterior.
Applet de Miguel Ángel Cabezón Ochoa bajo licencia Creative Commons.