3. Vamos a experimentar
Álvaro se levantó y sacó una moneda de un baúl. Se la tiró a Manu y le dijo: "A ver qué te parece esto".
Manu cogió la moneda. Era un dolar bastante brillante. Manu lo lanzó al aire y salió cruz.
- "¿Qué quieres que mire?"- dijo Manu.
- "Es una moneda trucada".
- "¿En serio? ¿Y siempre sale cruz?"- dijo mientras volvía a lanzar la moneda.
- "No, no siempre, pero sale con más frecuencia que en una moneda normal".
- "¿Y con qué probabilidad sale cruz?"
- "Pues no lo sé" - dijo Álvaro- "Pero podríamos calcularlo, ¿no?".
Hicieron diez lanzamientos y obtuvieron 6 cruces y 4 caras.
- "Si sale cruz con una frecuencia de 6 de cada 10, la probabilidad es 0,60"- dijo Álvaro.
- "No estoy seguro... creo que deberíamos hacer más tiradas".
Importante
La frecuencia absoluta (fi) de un suceso es el número de veces que ocurre.
La frecuencia relativa (Fi) de un suceso es la proporción de veces que ocurre. La obtenemos dividiendo la frecuencia absoluta entre el número total N.
Manu y Álvaro siguieron lanzando la moneda y apuntaron los resultados, de forma que obtuvieron los siguientes resultados:
|
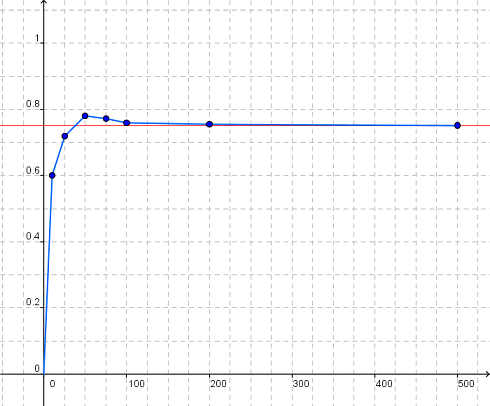
"Sale cruz" |
Nº tiradas N |
Frec. abs. fi |
Frec. relat. Fi = fi / N |
| 10 |
6 |
0,6 |
|
| 25 |
18 |
0,72 |
|
| 50 |
39 |
0,78 | |
| 75 |
58 |
0,773 |
|
| 100 |
76 |
0,76 |
|
| 200 | 151 |
0,755 |
|
| 500 |
376 |
0,752 |
Si representamos estos datos, veremos que la Frecuencia Relativa se va acercando al valor 0,75.
Importante
AV - Actividad de Espacios en Blanco
|
| Fair dice view 1, de andreas.hopf, CC by-nc 2.0 |
Para comprobar si un dado tetraédrico (como el primero de la foto, pero con un número del 1 al 4 en cada una de sus caras) está trucado vamos a usar la Ley de los Grandes Números y comprobemos si todas las caras del dado tienen la misma probabilidad de salir.
Completa los espacios en blanco con la cifra decimal que corresponda. Utiliza todos los decimales necesarios en cada caso.
| Nº de la cara | ||||||||
| 1 |
2 |
3 |
4 |
|||||
| Tiradas |
fi |
Fi |
fi |
Fi |
fi |
Fi |
fi |
Fi |
| N=100 |
27 | 27/100=0,27 |
25 |
|
25 |
|
23 |
|
| N=500 |
145 |
145/500=0,29 | 110 |
|
128 |
|
|
0,234 |
| N=1000 |
298 |
0,298 |
203 |
|
248 |
|
251 |
|
| N=10000 |
3003 |
0,3003 |
1997 |
|
|
0,2501 |
2499 |
|
a) ¿Todas las caras tienen la misma probabilidad de salir?, es decir, ¿crees que el dado está trucado? (responde sí/no) .
b) Si jugaras con este dado a qué cara apostarías? A la cara número .
c) Con los datos que tenemos, ¿podemos decir que la probabilidad de que salga el 4 es de 0,25? (responde sí/no) .