2. ¡Hagan sus apuestas!
Álvaro y Marta llegaron con unos aperitivos y unas bebidas y preguntaron a sus amigos:
- "¿Habéis decidido ya a qué vamos a jugar?"
- "Aún no. Estábamos haciendo algunas apuestas entre nosotros".
- "Me apunto". - Dijo Marta.
- "De acuerdo. ¿Cuánto apuestas a que la próxima carta que saco es un número?".
- "No es justo, la probabilidad de que saques un número es muy alta".
- "¿Estás segura? ¿Se puede calcular?"
- "A ver... en total hay 52 cartas, y de ellas 40 son números. Por lo tanto tienes una probabilidad de 40 a 52".
- "Entonces la probabilidad de sacar un número es..."
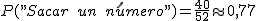
- "Tenías razón ¡tengo más del 75% de probabilidad de sacar un número!".
Ley de Laplace: Si en un experimento aleatorio todos los sucesos elementales son equiprobables (es decir, tienen la misma probabilidad de suceder), la probabilidad de un Suceso Aleatorio A se puede calcular como:

Si estamos sacando una carta de una baraja podemos usar la Ley de Laplace para calcular probabilidades, ya que la probabilidad de sacar una u otra carta es la misma.
La probabilidad de sacar un 7 será:
- El número de casos favorables es 4, porque hay cuatro 7 en la baraja.
- El número de casos totales es 52, porque hay 52 cartas en la baraja.
P("Sacar un 7") = 4/52 ≈ 0,08
Completa los siguientes espacios usando la Ley de Laplace. Redondea los resultados a dos cifras decimales.
- P("Sacar el Rey de Corazones") = / 52 ≈
- P("Sacar una carta de Diamantes") = / 52 =
- P("Sacar una carta negra") = / 52 =
- P("Sacar una carta que no sea ni una figura ni sea de picas") = / ≈
En la escena siguiente, describen el suceso y dan la probabilidad del mismo, tú tienes que elegir la flecha que se ajusta a dicha situación.

|
| L0V3, de Pedrisho!, CC by-nc-nd 2.0 |
Según lo que hemos visto antes, la probabilidad de sacar una Figura será 12/52 ≈ 0,23 mientras que la probabilidad de sacar una carta de Corazones será de 13/52 = 0,25.
Si juntamos esos dos sucesos, ¿podemos decir que la probabilidad de sacar una Figura de Corazones será la suma de esas dos probabilidades?
P("Sacar una Figura") + P("Sacar una carta de Corazones") = 12/52 + 13/52 = 25/52 ≈ 0,48
Pero sabemos que P("Sacar una Figura de Corazones") = 3/52 ≈ 0,06. ¡Algo falla!
Vamos a descubrir por qué no nos ha dado el resultado que nos parecía lógico, para ello veamos las cuatro operaciones que podemos hacer con dos sucesos:
- UNIÓN: La unión de dos sucesos está formada por los elementos que pertenecen a alguno de los dos, o a los dos a la vez. La representamos por AUB.
- INTERSECCIÓN: La forman los elementos que pertenecen a la vez a los dos sucesos. La representamos por A∩B.
- DIFERENCIA: Los elementos de A-B son aquéllos que pertenecen a A, pero que no pertenecen a B.
- COMPLEMENTARIO: El complementario de un suceso A está formado por todos los elementos del espacio muestral que no pertenecen a A. Lo representamos por AC.
Volvamos a usar los sucesos A = "Sacar una Figura" y B = "Sacar una carta de Corazones".
Por otra parte tenemos los sucesos:
C = {1-C; 2-C; 3-C; 4-C; 5-C; 6-C; 7-C; 8-C; 9-C; 10-C}
D = {1-C; 2-C; 3-C; 4-C; 5-C; 6-C; 7-C; 8-C; 9-C; 10-C; J-C; Q-C; K-C; J-D; Q-D; K-D; J-T; Q-T; K-T; J-P; Q-P; K-P}
E = {J-C; Q-C; K-C}
F = "Los números del 1 al 10 de Trébol, Diamantes o Picas"
Completa los siguientes espacios con una letra de la C a la F, usando los sucesos anteriores.
- El suceso AUB es . Su probabilidad es / 52 ≈
- El suceso A∩B es . Su probabilidad es / 52 ≈
- El suceso B-A es . Su probabilidad es / 52 ≈
- El suceso (AUB)C es . Su probabilidad es / 52 ≈
Si tenemos dos sucesos A y B de los que conocemos su probabilidad, se cumple que:
- P(AUB) = P(A) + P(B) - P(A∩B)
- P(AC) = 1 - P(A)
- P(A-B) = P(A) - P(A∩B)
 |
| come quando fuori piove, de auro, CC by-nc-nd 2.0 |
Ana estaba entretenida con las fichas del Scrabble. Separó unas cuantas letras y dijo a sus amigos:
Tengo aquí las fichas A, B, C, D y E. Las letras A y E valen 1 punto cada una, las letras B y C valen 3 puntos, y la letra D sólo vale 2 puntos.
Vamos a usar los sucesos X = "Sacar la A, la B o la C", Y = "Sacar la B, la C o la D" y Z = "Sacar una ficha de tres puntos".
Sólo os diré que,
- P(X) = P({A, B, C}) = 0,7
- P(Y) = P({B, C, D}) = 0,8
- P(Z) = P({B, C}) = 0,5
a) Antes de empezar, ¿qué suceso sería la unión de los dos primeros?
|
X U Y = {A, B, C, B, C, D}
| |
|
X U Y = {A, B, C, D}
|
|
X ∩ Y = {B, C}
| |
|
X ∩ Y = {A, D}
|
