2.1. Ven, acércate...
Al químico y filósofo irlandés del siglo XVII, Boyle-Mariotte, se debe, entre otro muchos resultados, la ley que lleva su nombre: "si un gas se mantiene a temperatura constante, su volumen es inversamente proporcional a la presión".
En el siguiente vídeo podemos disfrutar de una justificación casera de dicha ley.
En la siguiente escena de GeoGebra disponemos de un gas depositado en un recipente y taponado por un émbolo que se desplaza verticalmente. Al aumentar la presión, el volumen del gas disminuye, y si la presión disminuye, aumenta el volumen. Para realizar dicha acción, debemos mover el punto negro que está situado en el eje horizontal.
La relación que existe entre el volumen "f(x)", expresado en litros, y la presión "x", expresado en Newton por cm2, viene dada por la función: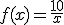 
.
Mueve el punto negro, y observa cómo al disminuir la presión, crece rápidamente el volumen. En la tabla que hay a la derecha, van apareciendo los valores de x y f(x).
AV - Actividad de Espacios en Blanco
a) Si la presión es de 0,01 N/cm2, el volumen será de litros.
b) Si la presión se acerca aún más a 0, es de 0,002 N/cm2, el volumen sería de litros.
c) Por último, para una presión de 0,00004 N/cm2, el volumen alcanza ya la magnitud de litros.
AV - Actividad de Espacios en Blanco
a) f(x) = 2x-3 se aproxima a .
b) f(x) = x2-3x+4 se aproxima a .
c) por la izquierda, es decir, para valores más pequeños que 2, f(x) = ent(x) se arpoxima a .
d) por la derecha, es decir, para valores mayores que 2,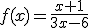 
se hace muy
.
Actividad
Si f(x) se acerca a l cuando x se aproxima al punto a, diremos que l es el límite de f(x) en el punto a.
Lo anterior se expresa de la siguiente forma: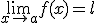 
.
Teniendo en cuenta la definición de continuidad que dimos en el apartado anterior, tenemos que f es continua en a si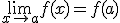 
.
Esto facilita muchísimo el límite de una función en punto para las funciones continuas en todo su dominio, que, como hemos visto, son la mayoría de las funciones elementales.
Calcular el límite de f(x)=x3+4x+7 cuando x tiende, por ejemplo, al punto -1, es muy fácil. Como f(x) es una función polinómica, por tanto continua en todo su dominio, basta con hallar f(-1).
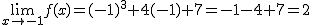
En el caso de la relación entre la presión y el volumen de un gas, es decir la función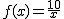 
, el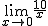 
no existe, porque al acercarnos a 0, tanto para valores mayores que 0, como para valores que 0, f(x) tiende a infinito.
En el siguiente tutorial se explica cómo podemos calcular límites de una función en un punto con la ayuda de Wiris.
Ejemplo o ejercicio resuelto
a)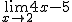 
b)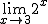 
c)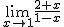 
d)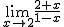 
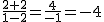. El límite es -4.