3. ¿A dónde vamos?
 |
Hasta ahora sólo nos ha preocupado el límite de una función en un punto, pero también nos podemos preguntar qué ocurre con f(x) cuando x, la variable independiente, se aleja mucho del origen. Es decir, qué ocurre con f(x) cuando x tiende a infinito, tanto a más infinito como a menos infinito.
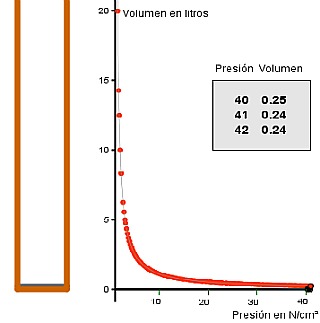
Volvamos al ejemplo de la presión y el volumen del gas,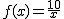 
. En el apartado anterior nos preocupó qué ocurría con el volumen, f(x), cuando la presión, x, se acercaba a 0. Ahora prestamos nuestra atención a qué ocurre con el volumen cuando la presión se hace muy grande. Es decir, cuánto vale:
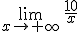
En el gráfico de la derecha podemos ver que si la presión es grande, el volumen es cada vez más pequeño, y tiende a cero. Es lógico, si x crece,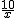 
decrece.
Además, se aprecia también que esa función tiene una asíntota horizontal en el eje de las X, es decir, y=0.
Actividad
Si f(x) se acerca a l cuando x se hace muy grande en valor absoluto, diremos que l es el límite de f(x) cuando x tiende a infinito.
Se expresa de la siguiente manera: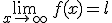 
.
Si x tiende a infinto sólo para valores positivos, diremos x tiende a más infinito. Y se escribe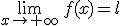 
. Cuando esto ocurre, la función tiene una asíntota horizontal en la recta y=l, para los valores positivos de x.
En el caso de que x tienda a infinito sólo para valores negativos, se dirá que x tiende a menos infinito. Se expresa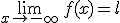 
. Cuando esto ocurre, la función tiene una asíntota horizontal en la recta y=l, para valores negativos de x.
En estas dos presentaciones, puedes ver cómo se comportan en el infinito las funciones polinómicas:
En las presentaciones hemos visto que el límite cuando x tiende a infinito puede ser infinito. Por ejemplo, en el caso de las funciones polinómicas y algunas racionales. Esto quiere decir que cuando x se hace muy grande en valor absoluto, f(x) también crece indefinidamente en valor absoluto.
Objetivos
 |
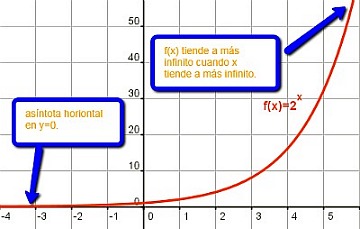La función exponencial ax, si a>1, presenta una asíntota horizontal cuando x tiende a menos infinito.
Por ejemplo, la función f(x)=2x tiene una asíntota horizontal en y=0, para los valores negativos de x. Es decir,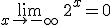 
.
Pero ese límite no es cierto si x tiende a más infinito. f(x)=2x se hace muy grande, cuando x se hace grande y es positivo. Por tanto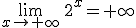 
.
En la imagen de la izquierda podemos ver la gráfica de f(x), y ver cómo los límites anteriores se ajustan a ella.
AV - Actividad de Espacios en Blanco
Consideremos ahora la función exponencial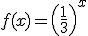 
.
Completa con las palabras: menos, horizontal, más, positivos, cero; los espacios en blancos que aparecen a continuación:
a) el límite de f(x) cuando x tiende a más infinito es .
b) f(x) tiene una asíntota en y=0, para los valores de x.
c) el límite cuando x tiende a infinito es infinito.
Pre-conocimiento
No todas las funciones tienen asíntotas. Ya hemos visto que las polinómicas no tienen. Tampoco el seno y el coseno. Por el contrario, la tangente tiene infinitas asíntotas verticales.
Las gráficas de las funciones que tienen asíntotas están muy condicionadas por ellas. En el siguiente vídeo podemos comprobarlo.
AV - Actividad de Espacios en Blanco
En la siguiente escena de GeoGebra aparecen las gráficas y la expresión analítica de cuatro funciones que puedes ir viendo si mueves el deslizador que tiene un punto verde. También puedes mover el punto naranja a lo largo de la gráfica.
Completa los siguientes espacios en blanco que contienen cuestiones relacionadas con esas funciones.
a) Las dos funciones que no tienen ningún tipo de asíntotas son y por ser las dos funciones polinómicas (escríbe sus nombres en orden alfabético).
b) g tiene una asíntota vertical en x= , y horizontal en y= .
c) El límite cuando x tiende a 0 por la izquierda de g(x) es infinito.
d) El límite cuando x tiende a menos infinito de g(x) es .
e) La única función que tiene asíntota oblicua es .
f) i tiene una asíntota vertical en x= , porque en ese punto se anula su denominador.
g) El límite cuando x tiene a 1 por la derecha de i(x) es infinito.
h) El límite cuando x tiende a menos infinito de h(x) es infinito.