4. El valor más absoluto
En el conjunto de los números reales tenemos una operación llamada valor absoluto. Esta operación no afecta a los números positivos, mientras que a los negativos les cambia el signo.
Esto nos pemite definir una función, valor absoluto, que tiene un efecto parecido: si el valor de f(x) es positivo, lo deja igual, en tanto que si f(x) es negativo, lo cambia de signo.
Si tenemos una función real f(x), podemos definir la función valor absoluto de f(x) como:
![]()
 |
| Reflejo, de gotencool, CC 2.0 by-nc-sa |
En realidad lo que hace esta función valor absoluto es "reflejar" la función f(x) en el eje de abscisas. Los trozos de la gráfica que estén por encima del eje, permanecerán igual, mientras que los que quedan por debajo obtienen su reflejo por encima del eje.
En la siguiente escena tienes un ejemplo. Si pulsas la casilla se ocultará el valor absoluto para que veas la función original. Puedes mover la función azul para ver cómo cambia su valor absoluto. También puedes cambiar la función escribiendo, por ejemplo: f(x)=2x-1, para ver cómo sería el valor absoluto de ésta u otra nueva función.
Mira las siguientes gráficas y elige las opciones adecuadas en cada caso.
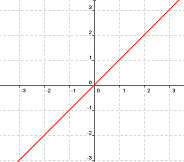 |
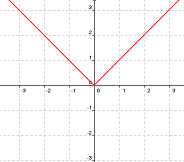 |
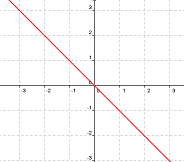 |
| f1(x) |
f2(x) |
f3(x) |
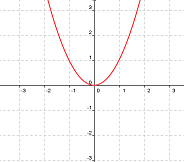 |
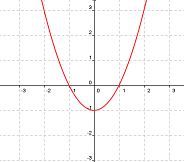 |
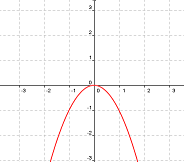 |
| g1(x) | g2(x) | g3(x) |
a) El valor absoluto de f1(x) es:
f1(x)
| |
f2(x)
| |
f3(x)
| |
f1(x)
| |
f2(x)
| |
f3(x)
| |
g1(x)
| |
g2(x)
| |
g3(x)
| |