3. Troceando funciones
Algunas funciones son caprichosas y pueden sufrir mutaciones de un instante a otro. Ya hemos visto que la función que determina la altura de la manzana que cae de un árbol es una función cuadrática. Pero si lo que dejamos caer es una pelota, ésta irá rebotando y alcanzando diferentes alturas dependiendo del tiempo que haya pasado.
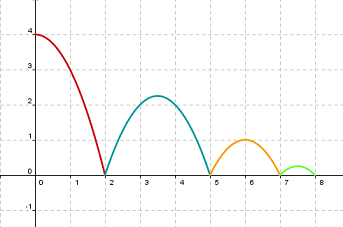
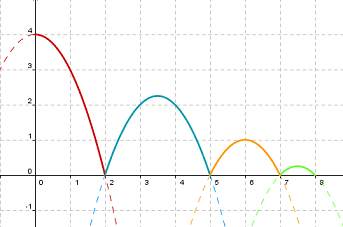
En las dos imágnes siguientes tienes un ejemplo de la altura que puede alcanzar un balón de baloncesto que rebota sucesivas veces. Como puedes ver en el gráfico de la derecha, en realidad se trata de trozos de parábola, es decir, trozos de funciones cuadráticas.
 |
 |
El trozo en el que nos encontremos depende de los valores de la x. Esta función podríamos expresarla de la siguiente forma:
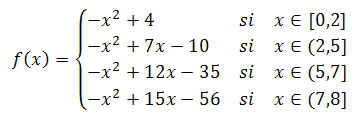
Para calcular el valor de la función en x=4, tendremos que irnos al segundo intervalo (2,5] y sustituir en ese trozo: f(4)=-16+28-10=2.
Además, recuerda que el signo 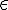 significa "pertenece". Por ejemplo, x
significa "pertenece". Por ejemplo, x 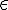 [0, 2] quiere decir que x está en el intervalo [0, 2].
[0, 2] quiere decir que x está en el intervalo [0, 2].
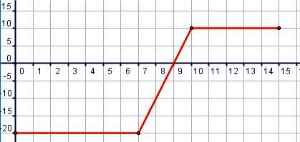 |
De las tres funciones definidas a trozos, que aparecen en la tabla, sólo tiene como gráfica la anterior.
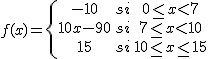 |
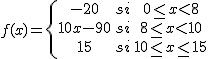 |
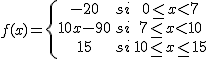 |
| a |
b |
c |
Para dibujar un trozo de una función en el programa Geogebra, debes utilizar el comando función[f,a,b], donde f es la expresión de la función, a es el extremo inferior del trozo y b el extremo superior.
Por ejemplo, si quieres trazar la gráfica de la función f(x)=x2-1 entre 0 y 10, escribe f(x)=función[x2-1,0,10]
Antes de terminar con una actividad, debes conocer dos funciones muy especiales que están definidas por pequeños trozos de funciones lineales.
|
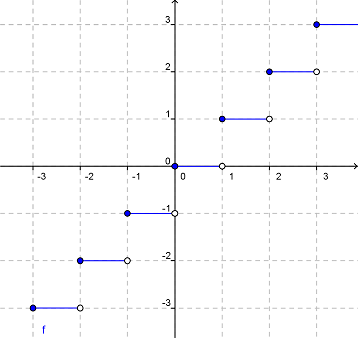
Función Parte Entera f(x)=E(x) |
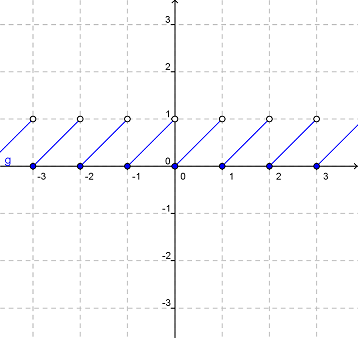
Función Mantisa g(x)=Mant(x) |
 |
 |
|
La función parte entera nos da el número entero
inmediatamente inferior a x. |
La función mantisa o parte decimal se obtiene al
restarle a un número su parte entera. |
Completa los espacios en blanco sobre la siguiente gráfica de una función a trozos:
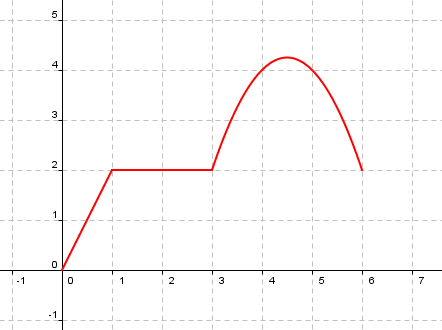
a) El dominio de esta función es D(f)=[ , ] y su recorrido R(f)=[ ,17/4].
b) La gráfica de la función pasa por los puntos ( ,0), (2, ), (5, ) y (6, ).
c) El primer trozo de la gráfica es y=2x para x 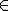 [
,
].
[
,
].
d) El segundo trozo es y=
, para x 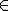 [
,
]
[
,
]
e) El tercer trozo es y=-x2+9x-
, para x 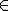 [
,
]
[
,
]