2. Es algo racional
 |
| Palanca, de César Rincón, CC 3.0 by-sa |
Hasta ahora hemos sumado, restado y multiplicado funciones polinómicas. Pero, ¿qué ocurre al dividirlas? ¿obtendremos un nuevo tipo de función?
Sí, son las llamadas funciones racionales, que al igual que ocurría con las polinómicas, también tienen una gran importancia en el mundo que nos rodea. Son numerosas las leyes físicas que vienen dadas por funciones racionales, como la Ley de la Gravitación Universal, o la conocida como Ley de la Palanca.
Esta última afirma que para levantar un cuerpo que pese 100 kg y que esté a 2 metros del punto de apoyo, necesito aplicar una fuerza que viene dada por la fórmula:
donde x es la distancia al punto de apoyo en metros. Con ello obtengo que, cuanto mayor sea esa distancia, menor es la fuerza que tengo que aplicar.
De hecho, siempre se recordará la famosa frase que dijo Arquímedes: "Dadme un punto de apoyo, y moveré el mundo".
Si te fijas, esta función se obtiene dividiendo dos funciones polinómicas, una de grado 0 y otra de primer grado.
Importante
Una función f(x) se llama racional si es el cociente de dos polinomios P(x) y Q(x).
En la escena de GeoGebra que tienes a continuación puedes ver cómo es la gráfica de una función racional. En este caso tienes representada la función f(x)=1/x. Si quieres puedes modificar los polinomios del numerador o del denominador. Por ejemplo, para dibujar la gráfica de la función f(x)=(3-x)/(x2-1), escribe:
- p(x)=3-x
- q(x)=x^2-1
(El símbolo ^ sirve para escribir potencias en GeoGebra y otros programas matemáticos)
A continuación puedes ver algunas características de las funciones racionales y cómo representarlas.
Objetivos
En la presentación anterior aparece el concepto de asíntota de una función. En la siguiente unidad se explicará con más detenimiento este tipo de rectas. Por ahora sólo diremos que una recta es asíntota de una función, si sus gráficas se aproximan de manera indefinida.
Por ejemplo, la función racional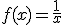 
, tiene como asíntotas la recta horizontal y=0, y la vertical x=0.
Una función polinómica no tiene asíntotas. Como hemos visto, muchas racionales sí las tienen.
AV - Actividad de Espacios en Blanco
, 
y 
.
- f(x) es una función de proporción .
- D(f)=
-{
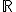} - R(f)=-{
}
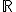- f(x) tiene una Asíntota Vertical en x= , y una Asíntota Horizontal en y= .
- f(x) es una función (creciente/decreciente)
- D(g)=-{
}
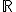- R(g)=-{
}
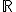- g(x) tiene una Asíntota Vertical en x= , y una Asíntota Horizontal en y= .
- g(x) corta al eje de abscisas en el punto ( ,0)
- D(h)=-{
,
}
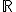- La gráfica de h(x) pasa por los puntos ( ,0), (0, ) y (-2, )