1. Orientémonos con sentido.
Vamos a comenzar a formalizar el concepto de vector haciendo uso de nuevo de los desplazamientos.
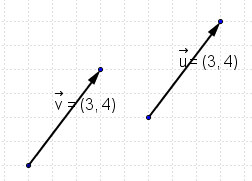
Supongamos que vamos circulando por la única carretera existente entre dos ciudades, ciudad A y ciudad B. Tenemos dos posibles opciones, a las que llamamos vectores, que no son más que distintas maneras de orientar el segmento AB.
1. Circulamos desde A hacia B. Lo representamos como vector 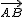 . El origen es el punto A y el extremo el punto B.
. El origen es el punto A y el extremo el punto B.
2. Circulamos desde B hacia A. Lo representamos como vector 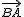 . El origen es el punto B y el extremo el punto A.
. El origen es el punto B y el extremo el punto A.
En los dos casos, la distancia entre los puntos A y B (ciudades A y B) es la misma y se denomina módulo del vector.
La situación presentada es una de las infinitas ocasiones en las que necesitamos hacer uso de los vectores.
Un vector fijo no es más que un segmento orientado entre dos puntos que denotaremos por 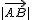 . El punto A se llama origen y el B extremo.
. El punto A se llama origen y el B extremo.
Atributos característicos de un vector fijo son:
* Dirección: Es la recta que pasa por los puntos A y B
* Sentido: Es el que va del origen al extremo del vector
* Módulo: Es la longitud del segmento AB. Se representa 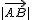
Cuando dos vectores fijos tienen iguales la dirección, el módulo y el sentido diremos que son equipolentes (o equivalentes).
Vamos a poner en práctica lo visto hasta el momento con dos escenas del proyecto Descartes elaboradas por Eva Mª Galán Solar.
En la Escena 1, puedes pulsar para activar las rectas que indican la dirección de los vectores.
En la Escena 2, debes clicar encima y arrastrar los puntos amarillos colocados en A, B, E y F.
| Escena 1. Para practicar: Dirección, Sentido y Módulo | Escena 2. Para practicar: Vectores equipolentes |
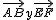 (de la Escena 1) tienen el mismo sentido.
(de la Escena 1) tienen el mismo sentido.
Verdadero Falso
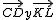 (de la Escena 1) tienen la misma dirección y el mismo sentido.
(de la Escena 1) tienen la misma dirección y el mismo sentido.
Verdadero Falso
Verdadero Falso
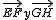 (de la Escena 2) son equipolentes.
(de la Escena 2) son equipolentes.
Verdadero Falso
¿"Dirección" prohibida o "sentido" prohibido?

| Vectores libres. Proyecto Descartes. |
Un vector libre está compuesto por un vector fijo y todos los vectores equipolentes a él. Cada uno de estos vectores fijos es un representante del vector libre.
Dicho de otro modo, un vector libre no es más que un vector fijo que se puede trasladar libre y paralelamente a sí mismo. Todos los representantes de un vector libre, tienen la misma dirección, el mismo sentido y el mismo módulo.
Los vectores libres se escriben entre corchetes 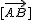 o con letras minúsculas,
o con letras minúsculas,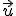 , ya que no hay dependencia de su origen y extremo, cualquier representante lo identifica.
, ya que no hay dependencia de su origen y extremo, cualquier representante lo identifica.
¿Cuántos vectores libres has obtenido con la agrupación anterior?
Cuatro, ¿verdad?. Los 17 vectores fijos, han quedado reducidos a tan sólo cuatro vectores libres. O sea, que en principio hay muchos vectores fijos pero en muchos casos representan el mismo vector libre, es decir, representan el mismo desplazamiento.
Hasta aquí bien, hemos visto la cara geométrica de los vectores. A continuación, veremos la cara algebraica de los mismos y, de aquí en adelante, trabajaremos en paralelo desde ambos mundos: "el geométrico (dibujos) y el algebraico (coordenadas)"
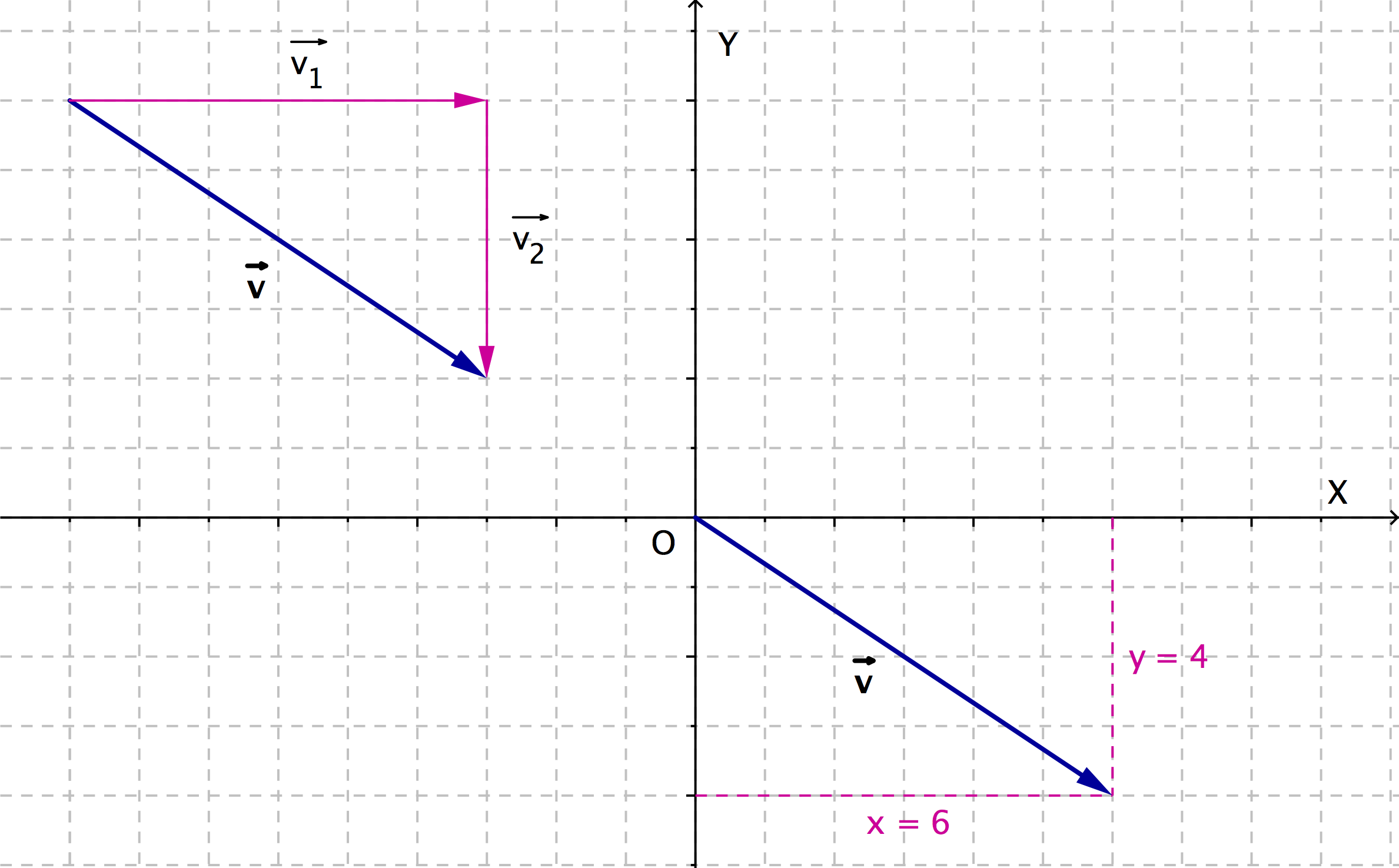
Ya sabes que los vectores indican desplazamientos desde un punto origen a un punto extremo. Desplazamientos que tienen dos componentes: la componente horizontal (hacia la derecha o hacia la izquierda) y la componente vertical (hacia arriba o hacia abajo). Cada uno de ellos es realmente un vector y la suma de ambos vectores indicará el desplazamiento total. Esta es la base sobre la que se sustenta la introducción de las coordenadas de los vectores y que representa la conexión entre los dos mundos: dibujos y coordenadas.
|
| Las coordenadas del vector v son (+6,-4) Desplazamientos: Horizontal x= +6 (hacia la derecha), Vertical y=-4 (hacia abajo) |
Si observas con detenimiento la escena anterior de Descartes (Vectores libres), comprobarás que lo que ocurre es que todos los vectores equipolentes representan exactamente los mismos desplazamientos, todos tienen las mismas coordenadas. Partiendo de distintos orígenes pero, al fin y al cabo, los mismos desplazamientos.
Apoyándote en el applet de Geogebra anterior, realiza las siguientes actividades:
(1) Desplazando únicamente el extremo del vector 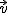 , obtén un vector equipolente a
, obtén un vector equipolente a 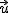
|
Comprueba si lo has realizado correctamente.
|
 es:
es:
|
(0,5)
| |
|
(4.5,0)
| |
|
(0,4.5)
|
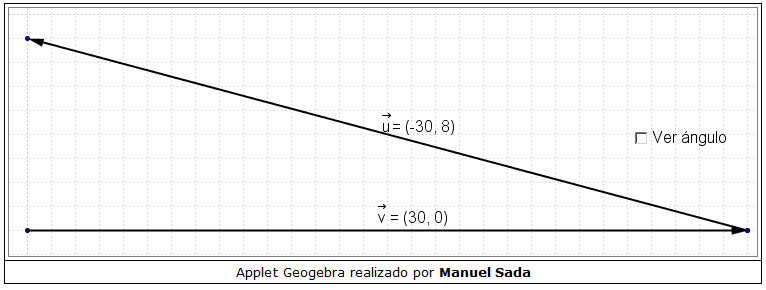
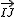 tienen el mismo módulo (miden lo mismo)
tienen el mismo módulo (miden lo mismo)
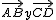 si que son equipolentes. Compruébalo.
si que son equipolentes. Compruébalo.