1.2. La sala de operaciones.

|
|
Imagen de Maldita la hora con licencia by-sa-2.0-deed
|
Siguiendo la flecha, tal y como se muestra en la imagen, hemos llegado a la sala de operaciones de los vectores.
Efectivamente, el lugar, donde operaremos con ellos.
Como ocurre con cualquier otro tipo de habitante del país de las matemáticas, como por ejemplo los números, los vectores también podemos sumarlos, restarlos, multiplicarlos por un número e, incluso, multiplicarlos entre ellos, como también veremos más adelante.
¿Y para qué vale sumar dos vectores?
Pues tiene mucha utilidad, pero simplemente citaremos para empezar un par de ellas.
¿Cómo despega un avión? Pues despega, mediante la suma de dos vectores de fuerza, uno correspondiente al desplazamiento hacia adelante (en horizontal) y otro correspondiente a la fuerza que tira de él hacia arriba (en vertical) de propulsión.
¿Quieres otra aplicación? Un ciclista ha realizado una ruta entre varios pueblos cercanos al suyo, pero de manera improvisada, y ha pinchado en el 5º municipio. Quiere conocer la trayectoria completa, la distancia recorrida y la distancia a la que se encuentra de su casa, puesto que el seguro que tiene, no le cubre asistencia, a distancias a su domicilio superiores a 75 km.
¿Cómo se suman y/o se restan vectores?
Gráficamente, la suma (resta) de vectores se puede realizar siguiendo dos métodos distintos. Por supuesto, por ambos métodos, se obtiene el mismo resultado.
* Métodos gráficos para realizar la suma de dos vectores.
+ Primer método (Regla del Paralelogramo)
Se traslada uno de los vectores (si fuese necesario), paralelamente hacia el otro hasta que sean concurrentes (tengan el mismo origen). Se prolongan los extremos, paralelamente, formando un paralelogramo. Finalmente, se traza la diagonal de dicho paralelogramo, que será el vector suma que buscamos.
+ Segundo método (Encadenamiento)
Se traslada uno de los vectores (si fuese necesario), paralelamente hacia el otro, hasta colocarlo a continuación del primero. Es decir, justo en el extremo del primero se coloca el origen del segundo, como si estuviésemos colocando eslabones de una cadena. Finalmente, se une el origen del primero con el extremo del segundo, dando lugar al vector suma que buscamos.
* Métodos gráficos para realizar la resta de dos vectores.
Observemos que restar dos vectores, 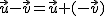 , es lo mismo que sumar el primero con el opuesto del segundo. Así, primero obtendremos el opuesto del segundo,
, es lo mismo que sumar el primero con el opuesto del segundo. Así, primero obtendremos el opuesto del segundo, 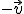 , y luego realizaremos la suma por cualquiera de los dos métodos anteriormente descritos.
, y luego realizaremos la suma por cualquiera de los dos métodos anteriormente descritos.
Al mismo tiempo, dijimos que las operaciones con los mismos podían realizarse en los dos mundos: en el geométrico (gráficamente) y en el algebraico, coordenadas (analíticamente)
* Método analítico para realizar la suma (y la resta) de dos vectores.
- La suma de dos vectores libres 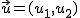 y
y 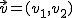 es otro vector libre que se obtiene sumando las componentes de los dos vectores dados:
es otro vector libre que se obtiene sumando las componentes de los dos vectores dados:
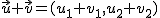
- La resta de dos vectores libres es igual a la suma del primero con el opuesto del segundo. La resta de dos vectores libres es otro vector que se obtendrá restando las componentes del segundo vector a las del primero:
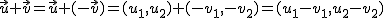
En el siguiente applet de Geogebra puedes poner en práctica lo aprendido sobre la suma y la resta de vectores. Activa/desactiva la casilla Mostrar coordenadas según te interese en cada caso. Para ver uno u otro método, mueve el punto en el deslizador correspondiente.
Para la resta de vectores no se incluirá ningún applet específico, puesto que no se considera necesario. Antes de realizar la resta, deberás obtener el opuesto del segundo vector y, finalmente realizar la suma.
Practica cuanto necesites con él.
|
|
| Applet de Geogebra. Luis Miguel Iglesias. Suma de dos vectores |
Los vectores tienen infinitas aplicaciones pero, especialmente, en la rama de la Dinámica dentro de la Física desempeña un papel crucial para el trabajo con Fuerzas. Veamos una aplicación de la suma de vectores, para el cálculo de la resultante de fuerzas.
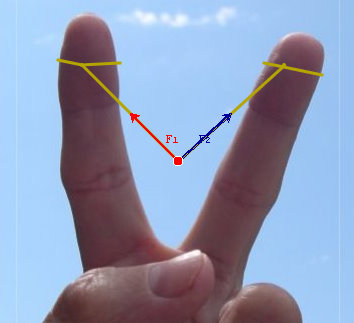
El tirachinas. Formamos con los dedos y una goma de escritorio un
tirachinas. La fuerza que ejercen las gomas dependen de la longitud
estirada. Ensaya distintos disparos al cielo en el plano vertical y
observa
el valor de la resultante.
Fíjate en la regla del paralelogramo para hallar la resultante.
Pulsa aquí para acceder a la escena de Descartes del proyecto Newton, donde se explica de manera detallada.
¿Cómo expresarías el doble de un desplazamiento determinado, haciendo uso de los vectores? ¿Y quedarte a mitad del camino de un determinado itinerario que hayas previsto? ¿Y realizar el mismo desplazamiento pero en sentido contrario?
Esto es posible efectuarlo de una forma cómoda mediante la multiplicación por escalar. En el primer caso bastaría con 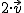 , en el segundo con
, en el segundo con 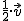 y en el tercero con
y en el tercero con 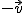
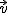 por un escalar, k (un número real), es un nuevo vector que escribiremos como
por un escalar, k (un número real), es un nuevo vector que escribiremos como 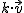 . Este vector tiene las siguientes características:
. Este vector tiene las siguientes características:
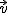
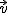 si k es positivo y el contrario si k es negativo.
si k es positivo y el contrario si k es negativo. 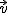 :
: 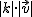
Dados los vectores 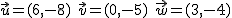 , realiza las siguientes operaciones, gráficamente, en un papel de cuadriculado y calcula las coordenadas.
, realiza las siguientes operaciones, gráficamente, en un papel de cuadriculado y calcula las coordenadas.
(1) 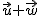
(2) 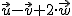
(3) 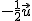
(4) 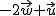
¿No conoces la historia de Vectorcito rojo y la Matriz feroz? Pues dice así ...
VECTORCITO ROJO Y LA MATRIZ FEROZ (Autor: David Gutiérrez Rubio)

|
| Imagen de peterme con licencia by-sa-2.0-deed |
Erase una vez un vectorcito que vivía con su familia generadora en su casita, V. Era un vectorcito muy joven, pues apenas acababa de cumplir un módulo. Tenía el sobrenombre de Vectorcito Rojo por ser una ferviente admiradora de Lindeloff, famoso comunista de la época.
Cierto día, su mamá la llamó: —“¡Eh, Vectorcito Rojo, ven aquí!. Quiero que lleves estas coordenadas a la casa W de tu abuelita, pues la pobre está muy sola desde que se ha restringido a un espacio de dimensión 1 , pero ten cuidado cuando vayas por el bosque Hom(V,W), pues hace tiempo que acecha una matriz muy, muy feroz.”
(...)
Compártelas con amigo/as y familiares. Les harán ver las matemáticas de otra manera.
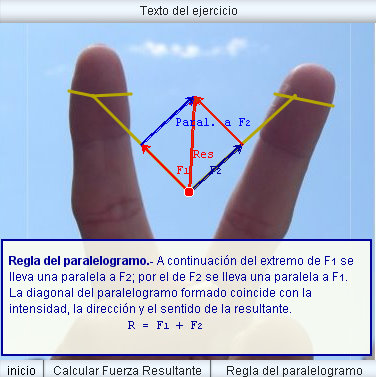
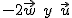 son opuestos.
son opuestos.