1.4. Dos vectores, un número.
Nada es lo que parece en matemáticas. Todo es natural en esta ciencia exacta pero, de vez en cuando, ocurren cosas que uno no espera hasta tal punto que podíamos catalogarlas como mutaciones.
 |
| Imagen de luis perez con licencia by-sa-2.0-deed |
Todas las operaciones que hemos visto en la sala de operaciones han dado como resultado un nuevo vector. La suma y la resta de vectores y la multiplicación de un vector por un número, dan como resultado un nuevo vector.
Pero, ésto no siempre es así. Vamos a tratar a continuación una operación en la que a partir de multiplicar dos vectores, obtenemos un número (un escalar), no un vector. De ahí que se conozca precisamente con el nombre de producto escalar, porque el resultado del producto es un escalar.
· El producto escalar de dos vectores 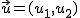 y
y 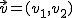 es un número. La fórmula que permite calcular su valor es:
es un número. La fórmula que permite calcular su valor es:
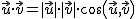
donde 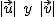 son los módulos de los dos vectores y
son los módulos de los dos vectores y 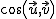 indica el coseno del ángulo que forman los orígenes de ambos vectores.
indica el coseno del ángulo que forman los orígenes de ambos vectores.
· La fórmula anterior permite obtener el ángulo que forman, conocidas las coordenadas de los dos vectores, simplemente despejando:
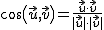
· Analíticamente, si conocemos las componentes (coordenadas) de los vectores, el producto escalar se obtiene como sigue:
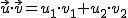
|
|
| Applet de Geogebra. Adaptación de Luis Miguel Iglesias (Original Manuel Sada). Producto escalar de dos vectores |
Algunas propiedades interesantes del producto escalar son:
- Dos vectores, no nulos,
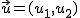 y
y 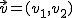 son perpendiculares, si y solo si su producto escalar vale 0. Es decir:
son perpendiculares, si y solo si su producto escalar vale 0. Es decir: 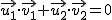
- El producto escalar de un vector consigo mismo es igual a su módulo al cuadrado. Dicho de otro modo:
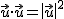
Terminamos la parte dedicada a vectores, con una aplicación de utilidad: el cálculo del punto medio de un segmento, concepto que podrás consolidar con la escena de Descartes que se encuentra tras el siguiente Importante.
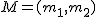 , del segmento cuyos extremos son los puntos
, del segmento cuyos extremos son los puntos 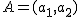 y
y 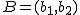 basta con aplicar la siguiente fórmula:
basta con aplicar la siguiente fórmula:
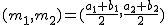
|
|
| Applet del Proyecto Descartes, elaborado por Pedro A. Pazos García. Punto medio de un segmento. |
Completa los huecos en blanco, ayudándote para ello de la escena de Descartes anterior.
- Las coordenadas de los puntos medios de los segmentos de color rojo son:
Ma=( , ), Mb=( , ) y Mc=( , )
- Las coordenadas (Px,Py) de P sabiendo que Q=(3,-5) y que el punto medio del segmento PQ es M(-1,3), son ( , )
Podrás practicar aún más con los apuntes y ejercicios resueltos disponibles en la web de Vitutor.

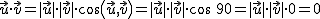
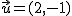 y
y 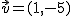 es igual a 8.
es igual a 8.
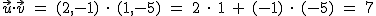
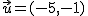 y
y 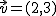 es igual a -13 y el ángulo que forman vale 135º
es igual a -13 y el ángulo que forman vale 135º