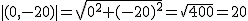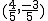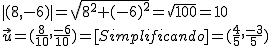1.1. Rutas y distancias.
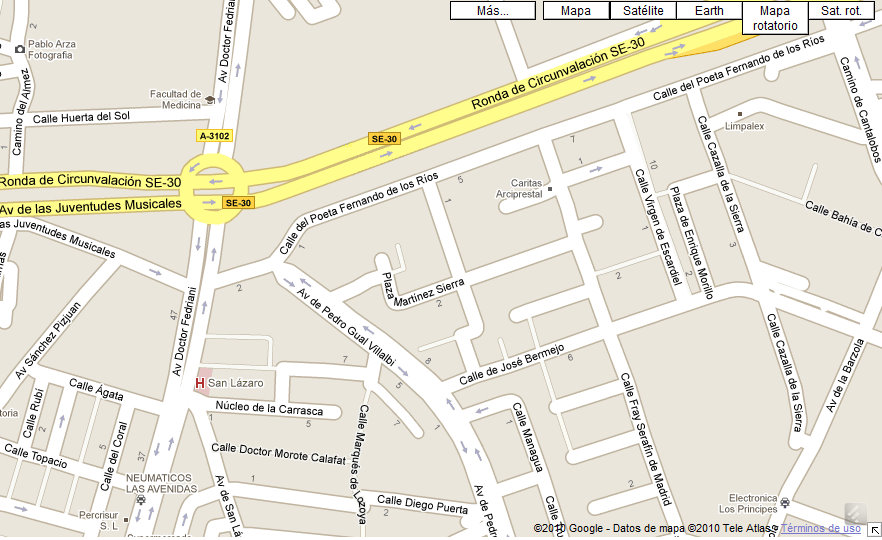
Para que un determinado servicio web, como puede ser Google Maps o cualquier otro servidor de mapas o un GPS, que tengamos en nuestro vehículo o en el propio móvil, nos pueda proporcionar una ruta en coche para "Ir desde: " "Hasta: " es necesario, previamente, etiquetar correctamente en la cartografía el/los sentido/s del tráfico permitido/s. De nuevo, son importantes los vectores en nuestras vidas así como el sentido de los mismos.
|
| Vectores: sentido del tráfico en la cartografía. Imprescindible para el cálculo de rutas en los navegadores |
Si este trabajo sobre la cartografía, no se ha realizado correctamente o, por ejemplo, el Ayuntamiento de una ciudad ha cambiado el sentido del tráfico de una determinada calle y la cartografía no lo ha actualizado, nos podemos encontrar con que el navegador de nuestro coche nos indique:
"Gire a la derecha" y ... ¡sorpresa! no es posible porque es sentido prohibido.
Fíjate hasta qué punto, es importante el sentido de los vectores en el cálculo de itinerarios/rutas.
Y ya que estamos con calles y rutas ...
¿Podrías decir cuánto mide una calle?
Efectivamente, la longitud del segmento que hay de un extremo a otro de la misma. Pues este es exactamente el concepto de módulo de un vector.
¿Y la distancia que recorres de un determinado punto a otro? ¿cómo la obtendrías?
Pues definiendo un vector, entre los puntos origen y destino (extremo) y calculando el módulo del mismo.
·
El módulo (o longitud) de un vector 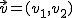 es igual a la longitud del segmento que une su origen y su extremo. El módulo, puede ser calculado de un modo sencillo (haciendo uso del Teorema de Pitágoras), mediante la siguiente fórmula:
es igual a la longitud del segmento que une su origen y su extremo. El módulo, puede ser calculado de un modo sencillo (haciendo uso del Teorema de Pitágoras), mediante la siguiente fórmula:
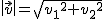
· Un vector es unitario si su módulo vale 1. A partir de cualquier vector, 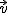 , podemos obtener otro vector,
, podemos obtener otro vector, 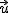 , que tenga la misma dirección y el mismo sentido que
, que tenga la misma dirección y el mismo sentido que 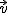 pero que sea unitario, es decir, con módulo igual a 1. Basta dividir, cada una de las componentes (coordenadas) de
pero que sea unitario, es decir, con módulo igual a 1. Basta dividir, cada una de las componentes (coordenadas) de 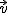 entre el módulo de
entre el módulo de 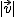 .
.
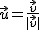
|
|
| Applet de Geogebra. Luis Miguel Iglesias. Módulo de un vector |
La prensa nuestra de cada día.
Una señora acude cada mañana a recoger el periódico a un kiosko de prensa que se ubica cerca de casa. Para ello, debe caminar, al salir de su vivienda ocho metros en dirección Este (hacia la derecha) y seis metros en dirección Sur (hacia abajo).
El vector que describe el trayecto diario de esta señora es el ( , ).
En total recorre metros.
 |
| Caminos opuestos, por mandoft con licencia by-sa-2.0-deed |
Dos tipos de vectores especiales son los vectores opuestos y los concurrentes:
· El opuesto de un vector 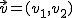 es otro vector que tiene el mismo módulo y dirección que
es otro vector que tiene el mismo módulo y dirección que 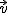 , pero distinto sentido.
, pero distinto sentido.
Se representa por 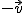 y sus coordenadas son
y sus coordenadas son 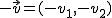
· Dos vectores son concurrentes si tienen el mismo origen, es decir, si parten del mismo punto.
La señora está enferma ...
y no puede ir a recoger el periódico. Realiza una llamada al kiosko para comunicarlo y, el kioskero, muy amablemente, decide llevárselo a su casa.
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso