1.2. Las tres juntas, y alguna más
¿Te acuerdas de Sinuhé? El pobre, aún irá camino de Asuán. Su jefe, Erastótenes, no coincidió con Pitágoras pues vivió casi cuatro siglos después que él. Pero seguro que, como hombre sabio y director de la biblioteca de Alejandría, era conocedor de su obra y por tanto del famoso teorema que lleva su nombre, el teorema de Pitágoras.
El teorema de Pitágoras dice que en un triángulo rectángulo ABC, hay la siguiente relación entre las longitudes de sus lados:
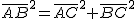
Es decir, la célebre frase: el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Recuerda, en la definición del seno, coseno y tangente no influía el tamaño del triángulo rectángulo que se construía sobre el ángulo no recto α.
Supongamos que la hipotenusa del triángulo ABC anterior mide 1. Es decir 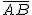 = 1.
= 1.
Completa, donde corresponda, con sen, cos y tg, los siguientes espacios en blanco.
α = 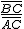
α = 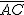
α = 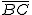
De la solución de la Autoevaluación anterior podemos deducir las siguientes dos igualdades.
1) sen2 α + cos2 α = 1
2) tg α = 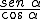
Para practicar las dos relaciones anteriores, aquí tienes el siguiente enlace.
Las dos igualdades anteriores son dos formas elegantes de relacionar las razones trigonométricas de un ángulo. En la primera se relacionana el seno y el coseno. Es decir, si conocemos una de ellas, podemos conocer la otra.
En la segunda, se relacionan las tres.
En la actualidad, y gracias al ya comentado uso de las calculadoras científicas, el manejo de estas fórmulas ha quedado bastante obsoleto. Cuando aún era necesario el uso de tablas para conocer las razones trigonométricas de un ángulo, el manejo de fórmulas como estas, y otras que veremos más adelante, era una herramienta muy útil.
Veamos a continuación una presentación donde se explica de forma breve cómo utilizar la calculadora para trabajar las razones trigonométricas.
| |
Volvemos al alquiler de plataformas para pintar fachadas de casas. Ahora nos preguntamos qué longitud mínima ha de tener el brazo telescópico de una grúa que se puede abrir hasta un ángulo de 70º, para poder alcanzar una altura de 10 metros.
Seguro que te ayudará a encontrar la solución de este problema realizar un dibujo esquemático de la situación planteada.
| |
Seguro que Sinuhé, en su peregrinación por tierras egipcias, se protegió más de una vez de las fuerzas de los rayos del Sol bajo la sombra de alguna de las magníficas pirámides construidas casi tres milenios antes.
Aún hoy nos impresiona su delicada belleza y armonía. Y nos seguimos haciendo el mismo tipo de preguntas que ya se hizo Sinuhé: ¿cómo pudieron ser construidas?
Como ya has podido ver en una presentación anterior, los arquitectos egipcios, para mantener la inclinación constante e igual en las cuatro caras de las pirámides, utilizaban el seked como medida para calcular la pendiente. Un seked es la razón que existe entre el avance y la altura de cada una de las caras de la pirámide.
En la pirámide que aparece en la imagen de la derecha, el seked sería el cociente entre 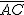 y
y 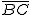 . Es decir, la inversa de la tangente del ángulo correspondiente al vértice A, del triángulo rectángulo ABC.
. Es decir, la inversa de la tangente del ángulo correspondiente al vértice A, del triángulo rectángulo ABC.
A la inversa del seno de un ángulo α, se le llama la cosecante del ángulo, y se escribe cosec α.
cosec α = 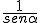
De manera similar se definen la secante y cotangente, como la inversa del coseno y de la tangente respectivamente.
sec α = 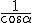 , y cotg α =
, y cotg α = 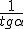
| |
| Pirámide de Kefrén de joma-joma, CC by-nc-nd 2.0 |
Nosotros no sólo nos preguntamos cuál es el seked de esa pirámide, también queremos saber cuál es el ángulo de inclinación de las caras de la pirámide.
Como ayuda para responder a estas dos cuestiones, basta con que te fijes en el gráfico que acompaña la Curiosidad de más arriba.
En varias ocasiones, hemos tenido que buscar un ángulo conocida su razón trigonométrica, es decir, hemos tenido que utilizar la tecla SHIFT de la calculadora científica.
A estos procesos se les llama arcos.
Por ejemplo, saber qué ángulo agudo tiene por seno 0,42, se le llama el arco seno de 0,42, y se escribe arcsen 0,42 = 24,83º.
De foma parecida se definen el arco coseno, y se escribe arccos α, y la arco tangente, que escribiremos arctg α.
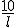 , por tanto , l =
, por tanto , l = 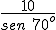 . Hallamos la sen 70º con la calculadora, operamos y obtenemos l = 10,64 metros, aproximadamente.
. Hallamos la sen 70º con la calculadora, operamos y obtenemos l = 10,64 metros, aproximadamente.
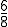 =0,75.
=0,75.
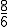 = 1,333...
= 1,333...