2. Mejor por intervalos
Como habrás podido comprobar en el apartado anterior, los estimadores puntuales sólo dan una idea aproximada del valor del parámetro a estimar, no conociéndose cómo de buena es la aproximación; ellos simplemente proporcionan el mejor número que pueda proponerse como valor del parámetro.
Por ejemplo decir que 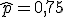 en el IES "Benito V." respecto al estudio de utilización de redes sociales, significa
que aproximadamente el 75% de todos los alumnos y alumnas del instituto participan en redes sociales a través de internet,
pero el término "aproximado" no se sabe si alude a un 1% arriba
o abajo, o a un 10% arriba o abajo. De hecho, no puede esperarse gran cosa
de un estimador.
en el IES "Benito V." respecto al estudio de utilización de redes sociales, significa
que aproximadamente el 75% de todos los alumnos y alumnas del instituto participan en redes sociales a través de internet,
pero el término "aproximado" no se sabe si alude a un 1% arriba
o abajo, o a un 10% arriba o abajo. De hecho, no puede esperarse gran cosa
de un estimador.
Los problemas anteriores eran de esperar pues realmente es demasiado
pedir que a partir de una muestra pueda calcularse el valor del parámetro
tan exactamente como si se tomara toda la población. En realidad lo que
importa es que el valor de la proporción muestral 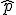 ,por
ejemplo, no esté demasiado alejado de
,por
ejemplo, no esté demasiado alejado de 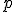 , y esto se comprueba con los intervalos
de confianza.
, y esto se comprueba con los intervalos
de confianza.
El objetivo es realizar afirmaciones del tipo: "la proporción media de todos los alumnos y alumnas no sé exactamente cuanto es, pero es casi seguro alguno de los valores 0,7 ≤ p ≤ 0,8, con una cierta seguridad".
La seguridad alude a la probabilidad de que la afirmación sea cierta, con lo que el problema de obtener intervalos de confianza para un parámetro radica en encontrar dos valores a y b tales que P (a ≤ p ≤ b) = 1-α, donde (a,b) es el intervalo de confianza para p, 1-α el coeficiente de confianza (c) del intervalo (usualmente próximo a 1) y α el nivel de error del intervalo (usualmente próximo a 0).
Aquí tienes un curioso vídeo donde se explica la estimación por intervalos de confianza de una proporción.
A la hora de estimar un parámetro poblacional, un intervalo de confianza es un rango de valores (calculado en una muestra) en el cual se encuentra el verdadero valor del parámetro, con una probabilidad determinada.
El nivel de
confianza, C, indica, en porcentaje, con qué proporción el intervalo de
confianza contiene el parámetro estimado.
El coeficiente de confianza, c=1-α, es la misma proporción en tanto por uno, c = C/100. En otras palabras, c es la probabilidad de que el intervalo de confianza contenga el parámetro estimado.
Al valor de α lo llamamos nivel de significación o de riesgo.
Al valor que resulta de restar el extremo superior del inferior del intervalo de confianza, lo llamamos margen de error.
Si α = 1 - c, y (a,b) es el intervalo de confianza se cumplirá lo que puedes ver en la siguiente escena de Descartes creada por Aurelio Casas.
VALORES CRÍTICOS
 |
|
Imagen de Guadalupe Cervilla bajo licencia Creative Commons |
Recuerda que cuando una distribución seguía una normal N(0,1), a veces no interesa calcular la probabilidad de que un parámetro esté en un intervalo, sino encontrar un intervalo que tenga cierta probabilidad.
Para ello necesitamos conocer los valores críticos Z1-α, -Z1-α, Z1-α/2 y -Z1-α/2 mirando el valor de la probabilidad en la tabla de la Normal.
Aquí tienes varias escenas de Descartes de Francisco Artigues para que repases el sentido que tiene el valor de Z.
Con la ayuda de la escena anterior o bien de la tabla de la Normal, contesta a las siguientes preguntas:
a) El valor crítico correspondiente a un nivel de confianza del 90% es ...
|
-1,64
| |
|
1,64
| |
|
1,645
|
|
(-2,2)
| |
|
(-2,17 , 2,17)
| |
|
(-2,15 , 2,15)
|
|
1, 51 %
| |
|
0,86896 %
| |
|
86,9 %
|
|
94 %
| |
|
19 %
| |
|
0,94257
|